Методология логистики. Модели перерабатывающего элемента. Модели накопительного элемента, страница 15

Оптимальный размер партии q_s в случае возможного дефицита груза на складе рекомендуется определять по формуле

Максимальный запас груза на складе при наличии дефицита

Время цикла (интервал времени между моментами прибытия партий груза на склад) определяется по формуле

Предварительно определим оптимальный размер заказа без учета возможности дефицита по формуле* Уилсона

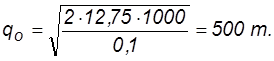
Найденное значение подставим в формулы (5.43) — (5.45) и рассчитаем параметры системы управления запасами с дефицитом груза:

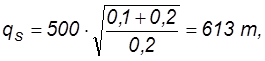
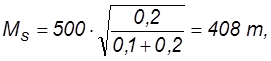
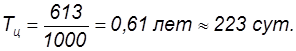
2) Модель, учитывающее изменение цен на материальные потоки. В реальных условиях цена на продукцию, а зачастую и транспортные расходы, имеют оптовые скидки, зависящие от размера партии. В этом случае возникает задача определения оптимального размера партии при оптовой скидке.

Допустим, что в год потребитель перерабатывает 1 млн. т груза. Транспортные расходы в данном примере не зависят от величины партии и составляют 25 руб. за тонну. В отличие от транспортных издержек цена единицы груза и затраты на содержание запасов на складе зависят от размера партии (табл. 5.1).

Таблица 5.1

Изменение цены продукции и затрат на хранение в зависимости

от размера партии

Поскольку условия поставок для разных размеров партии различны, расчеты необходимо выполнять для трех случаев. Предварительно определим размер партии по формуле Уилсона. При цене 2,50 руб.

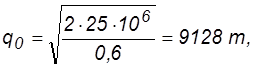
при цене 2,0 руб. q₀=11180 т и при цене 1,5 руб. q₀=12909 т. Поскольку основным критерием эффективности системы управления запасами являются суммарные годовые затраты, определим влияние на них покупной цены продукции. Для этого используем следующую формулу:

где С₁ — цена единицы закупаемой продукции.

При цене продукции 2,5 руб. годовые затраты составят

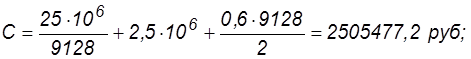
при цене 2,0 руб. — С = 2044721 руб. и при цене 1,5 руб. — С =1503873 руб.

Так как наименьшие годовые затраты достигаются при закупке продукции партиями по 20000 т и более, то делаем вывод о рациональности именно такого режима снабжения.

3) Модель ЛС, предполагающей наличие складов у потребителя и у поставщика материального потока. Следовательно, поставщик также несет затраты, связанные с хранением груза на складе. Эти затраты влияют на цену продукции, которую устанавливает поставщик и которая определяется размером поставляемой партии.

Допустим, что годовой спрос потребителя составляет 10000 вагонов, транспортные расходы составляют 2 тыс. руб. за вагон, цена груза в одном  вагоне составляет 14 тыс. руб., а затраты на содержание запасов у поставщика составляют 40% от стоимости одного вагона, а у потребителя — 45%. Требуется определить цену продукции, которую должен установить поставщик, если потребитель заказал партию из 45 вагонов.

Затраты на содержание продукции у потребителя составляют 45% от стоимости груза в вагоне, то есть i = C₁ × 45% = 14000 × 0,45 = 6300 руб. Тогда оптимальный размер партии поставки для потребителя составит

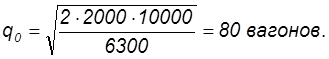
Однако ввиду транспортных ограничений и технологических условий производства (которые в явном виде не учитываются формулой расчета оптимальной партии), потребитель принимает решение о поставках партиями по 45 вагонов. В этом случае поставщик определяет цену, исходя из затрат на содержание запасов на своем складе по формуле

где i¢ определяется по из формулы Уилсона. Выполнив необходимые преобразования, получим следующую расчетную формулу для определения затрат на хранение продукции на складе: