Методология логистики. Модели перерабатывающего элемента. Модели накопительного элемента, страница 11

После подстановки в (5.27) получим

Заметим, что срок доставки груза исчисляется до момента поступления его на склад получателя.

Предприятие, изготовляющее продукцию, и ее потребитель могут поставить условие перед железной дорогой, регламентированное договором на эксплуатацию подъездного пути, подавать вагоны на грузовой фронт в количестве не более :    

Наконец, может действовать ограничение на по вместимости железнодорожных путей :

или по вместимости склада :

Проанализировав все ограничения, оставляют наиболее сильные. Задавшись видом распределения плотности вероятности , можно дифференцировать выражение функционала (5.25). Затем из уравнений

и

с учетом ограничений (5.28) – (5.31) нетрудно определить оптимальные параметры  и . Может оказаться успешным при оптимизации  и  подход, основанный на направленном переборе переменных. Такой алгоритм эффективен при значительном числе ограничений, налагаемых на  и и нелинейной функции цели.

Пусть в итоге статистического анализа определен вид распределения плотности вероятности как равномерно распределенной случайной величины , где  и  - параметры закона распределения. После подстановки величины  в выражение (5.25) и соответствующих преобразований получим:

Решая уравнение (5.33) относительно , имеем

Подставив выражение (5.35) в (5.33), рассчитаем величину резервного запаса

Соответственно преобразуется ограничение (5.28):

Напомним, что тарифный параметр  включает: удельные затраты на маневровые операции по подаче и уборке вагонов на грузовой фронт; затраты, связанные с начальными и конечными операциями при оформлении документов, приемом и выдачей грузов; приведенные затраты, связанные с пребыванием груза на колесах. Все перечисленные виды затрат имеют обратную зависимость от величины транспортной партии груза .

Продолжительность производственного цикла предприятия рассчитывается по известной величине :

Последняя формула связывает производственные параметры  и  c транспортными: уровнем тарифа и удельными затратами, связанными с простоем вагонов . Подстановка выражений (5.35) и (5.36) в (5.34) позволяет рассчитать затраты при реализации оптимальных параметров  и .

Укажем, что при случайном характере поступления порожних вагонов на подъездной путь предприятия, изготовляющего готовую продукцию, появляются время ожидания вагонами начала выполнения грузовых операций и связанные с этим фактором затраты . Данное обстоятельство необходимо учитывать при построении модели.

Развивая концепцию системного подхода при создании экономико-математической модели ЛЦ, уместно поставить еще одну проблему – определить оптимальную перерабатывающую способность грузовых фронтов  и  соответственно на складах производителя и потребителя (можно принять . Тогда в целевую функцию включаем затраты на амортизацию и ремонт погрузочно-разгрузочных машин (ПРМ)

и затраты, связанные с ожиданием вагонами выполнения грузовых операций,

где  - годовые отчисления на амортизацию и ремонт одной ПРМ;  - часовая производительность ПРМ;  - среднее время ожидания (определяется по теории массового обслуживания).

С учетом (5.39) и (5.40), опуская промежуточные преобразования, получим следующее выражение целевой функции:

Затем из уравнения  находим

где

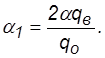
Значение  должно удовлетворять ограничениям (5.29), (5.31) и (5.37).

Анализ формулы (5.42) показывает, что с ростом перерабатывающей способности грузового фронта  уменьшается резервный запас груза , увеличиваются среднее число вагонов и масса груза в подаче. Это отвечает физической природе управляемого процесса.