Озон. Физика и химия озона. Химия атмосферного озона. Стратосферный озон и особенности его распределения, страница 29

Таким образом, происходит исключение  спектра зондирующего излучения и параметра, связанного с g-факторами, из данных, используемых для расчета концентрации определяемой газовой составляющей. Очевидно, для применимости подхода должны выполняться два условия: , в области длин волн, используемых для расчета концентрации. Иными словами, полуширина сглаживающего фильтра должна намного превышать полуширины линий поглощения, а в зондирующем излучении, относящемся к рабочей области спектра, должны отсутствовать структурные элементы с шириной, сравнимой с шириной линий поглощения определяемых газовых компонент. Точнее, такие элементы должны отсутствовать в разности логарифмов спектра реального зондирующего излучения и спектра источника, зарегистрированного ранее (возможно, в других условиях).  В случае озона возможны два варианта применения методики: а) использовать наличие малоинтенсивных структурных особенностей в спектре поглощения вблизи его максимума и б) использовать практически весь диапазон длин волн, занимаемый полосой Хартли. Ясно, что в первом случае методика окажется слабо чувствительной к озону из-за малости величин , во втором проблемой является необходимость измерения сигналов  в довольно широком интервале длин волн с малым шагом по длине волны. Именно эти сложности приводят к снижению точности измерения концентрации озона по методике OPSIS [54].

Влияние случайных ошибок измерений сигналов

Примем вполне  естественное предположение, что ошибки измерений сигналов  на каждой рабочей длине волны имеют случайный характер,  и результаты измерений на разных длинах волн не коррелированны друг с другом. Это означает, что имеют место равенства , если . Здесь суммирование при расчете средних ведется (в отличие от предыдущих случаев) по совокупности многократно повторяющихся измерений сигналов на длине волны  или по совокупности многократно повторяющихся пар измерений сигналов на длинах волн  и . Очевидно, что, согласно (11.8), аналогичные соотношения справедливы и в отношении величин : , если . Обозначим дисперсию случайной величины  . Тогда для дисперсии величины X, порожденной флуктуациями величин , можно получить [76]

                            .

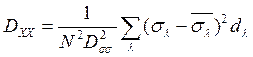Здесь N – число рабочих длин волн. Если дисперсии  на всех длинах волн - величины одного порядка,  можно записать

                                       ,

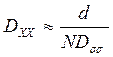где

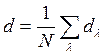                                         -                                                                                                  (11.20)

среднее значение дисперсии значений . Для относительного среднеквадратичного отклонения  измеренных концентраций озона имеем

                                          .

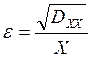Остается только выразить случайную ошибку в через относительные ошибки измерений сигналов  и  и связать дисперсию  с дисперсией сигналов. Согласно (11.8), (11.10) и с учетом малости ошибок измерений, погрешность величины  равна

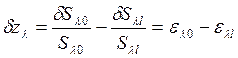                                              -                                                                 (11.21)

разности относительных погрешностей измерения сигналов. Отсюда при вполне естественном предположении о некоррелированности ошибок  и  находим

                                           ,

где

                                       ,     -

относительные дисперсии измерений сигналов, которые оцениваются в ходе непосредственных измерений. Следовательно,

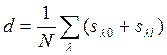                                          .                                                                                        (11.22)

Приведенные выражения связывают относительные дисперсии измерений сигналов на рабочих длинах волн с дисперсией  рассчитываемой концентрации озона.

Здесь имеет смысл вернуться к проблеме возможного несовпадения спектров зондирующего излучения на опорной и рабочей трассах. Ранее отмечалось, что величина  является удобной количественной оценкой качества юстировки трассового измерителя и стабильности его юстировки во времени. На самом деле эта величина никогда не может быть обращена в ноль из-за случайных ошибок измерений сигналов. В частности, если  (несовпадение в спектрах отсутствует), согласно (11.20)-(11.22) имеем