Соответствующие программы на языке MATHCAD даны в ПРИЛОЖЕНИИ 2.
2.8 Сетевые модели катастрофических последствий отказов.
Предлагается отказы в сложной технической системе трактовать как случайно выполненные «работы», определённая последовательность которых может приводить к катастрофическим последствиям (пожар, взрыв и т.п.). Образуется сетевой график таких «работ» - отказов. Сетевые графики планирования обычных работ хорошо изучены и могут служить эффективной моделью прогнозирования и оценки вероятности возможной катастрофы.
Например, на рис.1 в виде сетевого графика показана последовательность отказов пяти элементов Z1, Z2, Z3, Z4, Z5 , которая приводит к взрыву.
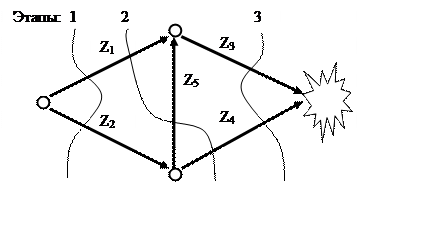
Рис. 7
Всего возможно 5! = 120 случайных последовательностей пяти отказов, но с допустимыми этапами выполнения сетевого графика согласуются только 11 последовательностей: 12453, 12534, 12543, 21453, 21534, 21543, 24153, 24513, 25134, 25143, 25413. Последовательность дана в лексикографическом порядке [1]. Вероятность катастрофы при разрушении системы определится отношением Рк = 11: 120 = 0.091666.
Очевидно, что с увеличением числа элементов системы m, сложность вычислений, в общем случае, будет возрастать как m!, поскольку это мощность множества перестановок, на котором происходит поиск решения. Для сравнения, в логико-вероятностных методах сложность вычисления вероятности безотказной работы системы возрастает как 2m , что меньше m! при m > 3. Поэтому, разработка алгебры кортежей и построение вероятностных оценок безопасности сложных систем на её основе будет в большей степени ограничена размерностью этих систем.
Остаётся обратиться к логико-статистическим методам . Однако, обычные статические логические модели для исследования сетевых структур плохо подходят. Фиксация отказа как события и включение его в сетевой график в виде выполненной «работы», при условии выполнения предшествующих, требует динамической логической модели, описания в виде конечного автомата, где элементы памяти, реагируют на динамические изменения логических индикаторов работоспособного состояния элементов (триггеры – защёлки).
На рис.8 приведен алгоритм, позволяющий оценить вероятность катастрофического завершения функционирования невосстанавливаемой cистемы из пяти параллельно включённых элементов и сетевой моделью катастрофы (рис.7).
|
Алгоритм вычисления вероятности катастрофических последствий отказов в технических системах доцент Краснов В.В. © версия от 10.04.2005 |
|
|
|
|
|
|
|
Число испытаний |
|
Результат статистической оценки вероятности выполнения сетевого графика, приведенного на рис7 |
|
Случайная последовательность из 5-ти отказов Предварительное обнуление меток "работ" Сортировка массива индексов элементов по 1-му столбцу Цикл расстановки меток дуг сетевого графика Фиксация очередного события - отказа элемента | Система рекуррентных уравнений, где Zi - метка | i-й "работы" на сетевом графике (очерёдность | вычислений определена функцией порядка - | этапы: 1, 2, 3 ) | | | | Ф - индикатор катастрофического завершения | | S - счётчик числа катастрофических исходов при N | разрушениях системы | Р - вероятность катастрофы Рис. 8 |
3. КОНТРОЛЬНІ ПИТАННЯ
до дисципліни "Надійність і діагностика електрообладнання"
1. Крива зменшення, показники надійності.
2. Значення забезпечення надiйностi, технічних систем.
3. Значення забезпечення життєвості, технічних систем.
4. Значення забезпечення безпеки, технічних систем.
5. Алгебра численностей.
6. Алгебра логіки.
7. Поняття міри, стохастичні мiри.
8. Аксіоматика теорії імовірностей Колмогорова.
9. Міри Хемминга та їх використання.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.