xi = í (9)
è0, если P (xi ) – ложно.
В этом случае вектор Х описывается двоичным целым числом.
Вектор Х определяет состояние элементов СЭЭС и порождает фундаментальное пространство состояний В мощностью 2m:
B = {X0, X1, …, Xi, …, Xk} (10)
где k=2m — 1. При такой нумерации векторов их значения соответствуют индексам, записанным в двоичном коде.
Высказывание P (Х): «Система работоспособна в состоянии XОB » является функцией алгебры логики от m логических переменных F(X). Эта функция выделяет в фундаментальном множестве В подмножество S, соответствующее работоспособным состояниям сложной системы:
S = {X Î B ê F(X) } (11)
Пример 1. Пусть судовая электростанция состоит из трех ДГ. Предельное состояние системы наступает при отказе двух ДГ. В этом случае
X = {x1, x2, x3} ;
B = {X0, X1, X2, X3, X4, X5, X6, X7},
где X0 = [000]; X1 = [001]; X2 = [010]; X3 = [011];
X4 = [100]; X5 = [101]; X6 = [110]; X7 = [111]
Область работоспособных состояний S = {Х3, X5, Х6, Х7}.
|
|
|
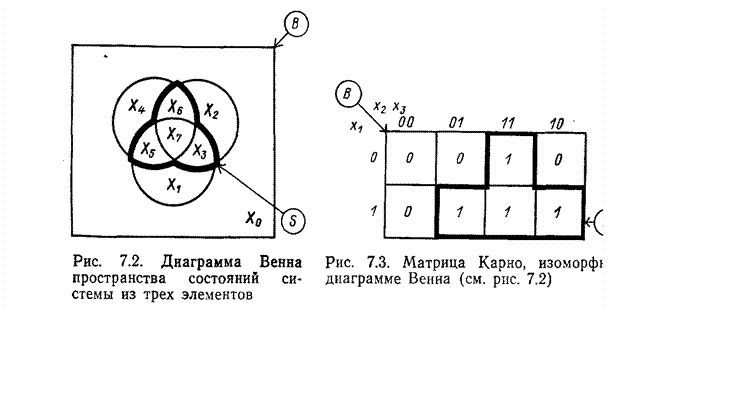 Более
наглядно эту область можно представить на диаграмме Венна (рис. 2) или на
соответствующей ей матрице Карно (рис. 3), откуда
Более
наглядно эту область можно представить на диаграмме Венна (рис. 2) или на
соответствующей ей матрице Карно (рис. 3), откуда
следует, что функция алгебры логики (ФАЛ)
F(X) = x1x2 Ú x1x3 Ú x2x3.
Из приведенного примера видно, что ФАЛ позволяет проводить логический анализ состояний системы, т. е. оценку ее работоспособности в конкретных состояниях, но количественные оценки показателей надежности пока сделать нельзя из-за отсутствия данных о вероятности появления каждого состояния системы. Правда, в этом случае иногда полагают все состояния равновероятностными и тогда вероятность безотказного состояния определится отношением мощности множества S к мощности множества В, что в приведенном примере дает значение 0.5.
1.4. Вероятностные меры надежности СЭЭС
Мерой может быть положительное конечное вещественное число. Например, масса, стоимость, объем, число элементов множества, абсолютная температура и т. п. Меры обязательно должны обладать свойством аддитивности, т. е. мера множества будет равняться сумме мер его элементов.
Обозначим введение меры вектора Х через оператор m(…):
m (X) = m (x1) + m (x2) + m (x3),
или в общем виде:
m
m (X) = S m (xi)
i=1
Согласно общепризнанной аксиоматике, введенной А.Н.Колмогоровым, вероятность определяется как нормированная мера в фундаментальном пространстве состояний В и обладает следующими свойствами:
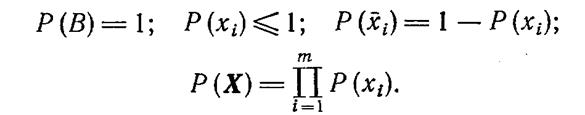
Если под P(xi) понимать вероятность работоспособного состояния i-го элемента системы, а под Р(Хj)—вероятность j-го состояния системы, то вероятность работоспособного состояния системы определится выражением
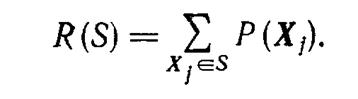
Если мерой эффективности электростанции является ее суммарная мощность, то она может быть вычислена для каждого состояния системы, кВт,
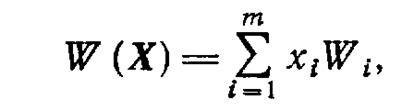
где xi—целочисленный индикатор по (9) автоматически исключает из суммы мощность отказавшего агрегата.
Математическое ожидание эффективности электростанции можно оценить как сумму произведений мощности в i-м состоянии на вероятность этого состояния в области работоспособных состояний, кВт,
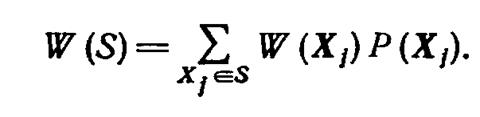
Если мерой эффективности СЭЭС является математическое ожидание выработанной ею энергии, то вероятности работоспособного состояния элементов должны задаваться как функции времени, например, при экспоненциальном законе распределения отказов
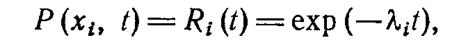
где li — интенсивность отказов i-го элемента системы.
Вероятность нахождения СЭЭС в одном из состояний (точке в пространстве состояние—время) определится произведением
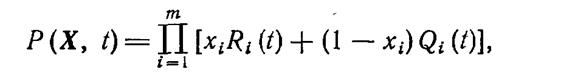
где Qi(t)=1—Ri(t)—вероятность отказа i-го элемента системы. Например, вероятность пребывания системы в состоянии x5 (см. рис. 7.2) вычисляется по формуле
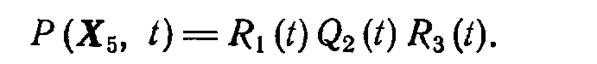
Математическое ожидание времени пребывания системы в данном состоянии за период наблюдения q определяется интегралом
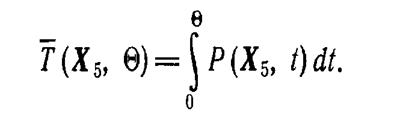
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.