Індивідуальний комплект навчально-методичних матеріалів з дисципліни "Надійність та технічна діагностика електрообладнання", страница 5

Таким образом, можно оценить математическое ожидание наработки электрической энергии СЭЭС до первого отказа:

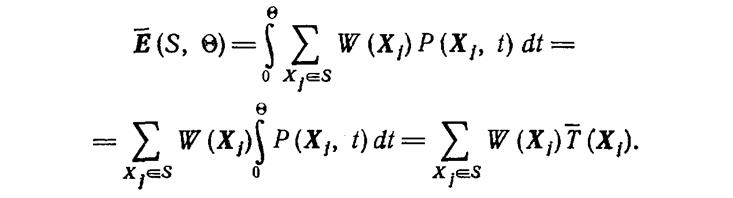
Если за q принять время нормальной работы (рис. 3.), то E будет соответствовать математическому ожиданию выработки электрической энергии за время “жизни” СЭЭС без учета восстановления.

В том случае, когда надежность СЭЭС определяют как комплексный показатель, включающий количественные оценки свойств C₁ ... С_п, возникает необходимость включения этих свойств в общую целевую функцию или ограничения. Чаще всего целевую функцию задают в аддитивной форме

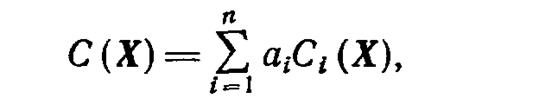
где a_i — весовые коэффициенты.

Если свойство включается в состав ограничений, то оно приобретает свойства логической переменной, например

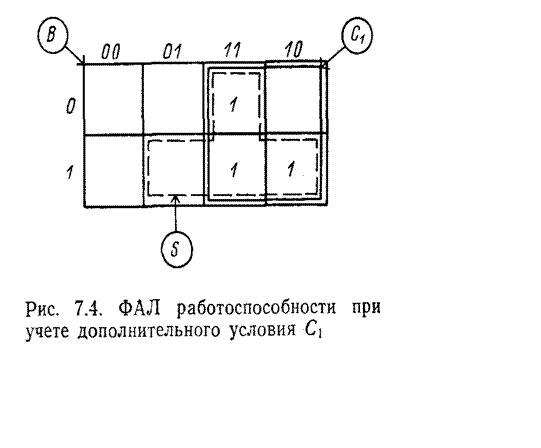
В этом случае свойство войдет в состав логических переменных, определяющих ФАЛ работоспособного состояния СЭЭС, например, в виде конъюнктивной формы

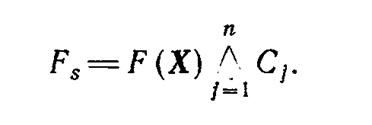
Если все свойства можно определить через вектор состояний СЭЭС, то ФАЛ работоспособного состояния по-прежнему будет задана на множестве В, т. е.

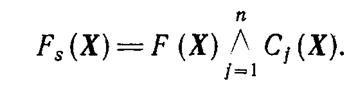
В ПРИЛОЖЕНИИ 1 приведены 34 варианта индивидуальных заданий для комплексной контрольной работы, содержащей основные разделы курса «теория надёжности». Ваш вариант задания должен совпадать с вашим порядковым номером в списке группы. Образец программы на языке MATHCAD для выполнения задания  и ответы даны в этом же ПРИЛОЖЕНИИ 1.

2.СТАТИСТИЧЕСКИЙ АНАЛИЗ СИСТЕМ

Статистические методы в надежности применимы для приближенной оценки параметров законов распределения отказов элементов и в имитационных методах исследования показателей надежности сложных систем. В последнем случае требуются весьма значительные ресурсы машинного времени и объемы памяти, поэтому часто встречающиеся алгоритмы статистической обработки данных и отдельные фрагменты процедур методов Монте-Карло иллюстрируют программы для ПМК. Программы для профессионального использования даны на языке  пакета MATHCAD-2001i.

2.1. Генераторы псевдослучайных чисел с равномерным распределением.

 Источниками псевдослучайных чисел в ЭВМ являются специальные алгоритмы. Как правило, любой закон распределения случайных чисел, воспроизводимый за счет имитации, строится на основе генераторов, дающих равномерное распределение в диапазоне 0...1.

Равномерное распределение характеризуется плотностью

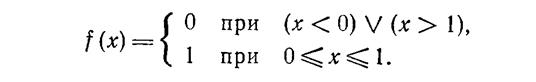
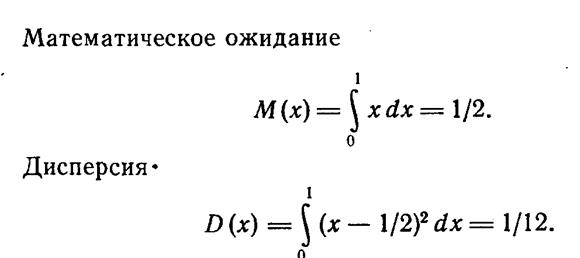
Рассмотрим алгоритм генерации псевдослучайных чисел, основанный на сложении двух случайных чисел по модулю 4, после сложения остается остаток от деления суммы на 4, который и принимают .за новое случайное число. Последующая нормировка (деление на 4) приводит к появлению чисел, изменяющихся в диапазоне 0...1.

Программа 7/34. Генерация псевдослучайного числа с равномерным распределением в диапазоне (0...1).

Инструкция: p=Р1;  0,5421019 =Р2; В/О; С/П; РХ = RAV. Повторное нажатие клавиши С/П приводит к появлению на индикаторе очередного случайного числа RAV.

Недостатком программы 6/34 является наличие в ней операторов условного перехода, что затрудняет ее использование в качестве подпрограммы, поскольку операторы 7 и 8 потребуют коррекции адреса перехода, если программа будет начинаться не с нулевого оператора.

Программа 8/34. Генерация псевдослучайных чисел с равномерным распределением в диапазоне (0...1)

Инструкция: х_о=Р9; В/О; С/П; РХ = х₁, С/П; РХ == х₂.; С/П; РХ=х (время счета около 5с).