Індивідуальний комплект навчально-методичних матеріалів з дисципліни "Надійність та технічна діагностика електрообладнання", страница 3

RNQ₁Q₂Q₃

 

1    N₀                                           1                   2

              N(t₁)  

          DN             N(t₂)

                                              3

                  Dt

 

        0        t₁          t₂                        t

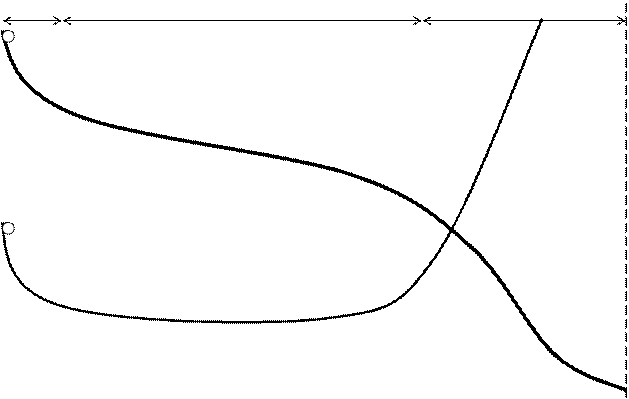
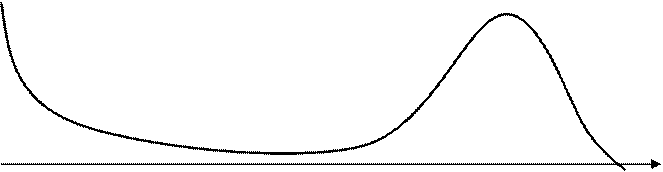
Рис. 1. Характеристики надёжности элементов,

определяемые при стендовых испытаниях

Наиболее полная характеристика безотказности R(t) — вероятность безотказной работы объекта за время t. По кривой убыли 1 эта вероятность определяется как статистическая оценка   

   R^*(t)= N(t)/No(1)

где символ «..^*» означает статистический характер величины; N₀—число объектов, взятых под наблюдение.

Вероятность того, что за время t объект откажет, вычисляется так:

      Q*(t)=[N₀-N(t)]/N_{0 .}

Всегда выполняется равенство R*(t)+Q*(t)=1, характеризующее нормированность вероятностной меры.

Плотность распределения f(t) (кривая 3) случайной величины Q(t) можно определить из кривой убыли 1:

f^*(t)=[N(t)-N(t+Dt)]/[N₀Dt] .                 (2)

С метрологической точки зрения все названные характеристики неудобны, поскольку в их определение входит значение числа элементов N₀. Поэтому в практических расчетах используют показатель l(t) —интенсивность отказов (кривая 2), который характеризует «смертность» среди объектов, имеющих «возраст» t. Статистическая оценка этого параметра

l^*(t)=[N(t)-N(t+Dt)]/[N(t)Dt].          (3)

Для его определения достаточен интервал времени Dt. Из простого сопоставления выражений (7.1)...(7.2) и (7.3) следует, что

     l^*(t)=f^*(t)/R^*(t)                            (4)

Если характеристики, представленные на рис. 1, считать непрерывными, то конечно-разностные формы (2) и (4) принимает вид дифференциальных уравнений

f(t)=dQ(t)/dt=-dR(t)/dt;    l(t)=-dR(t)/[R(t)dt].

Последнее выражение путем разделения переменных приводим к дифференциальному уравнению l(t)dt=-[R(t)]^-1dt, откуда следует важное соотношение

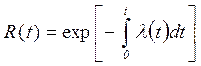                                   (5)                                   

Значение данного выражения заключено в том, что для многих элементов технических систем на участке нормальной работы Q₂ показатель интенсивности отказов можно принять за постоянную величину, которую обычно приводят в паспортных данных электроэнергетических установок и элементов судового электрооборудования:

R(t)=exp(-lt),  при l=const.                (6)    

1.3. Теоретико-множественные и логические модели надежности СЭЭС

Сложные технические системы, к которым относятся СЭЭС, способны выполнить заданные функции несколькими способами, что обеспечивает работоспособность при отказе отдельных элементов. Набор элементов, входящих в состав СЭЭС, является конечным, счетным множеством и может быть задан списком

X={x₁, x₂, ..., x_i, ...,x_m},                 (7)   

где Х—множество элементов, образующих СЭЭС, х_i—индикатор i-го элемента, принадлежащего множеству X, что обозначают через символ принадлежности О так: x_iОX.

Множество Х характеризуется мощностью m—числом своих элементов.

Относительно элементов СЭЭС могут быть высказаны различные утверждения, они становятся истинными или ложными в процессе исследования надежности СЭЭС. Например, высказывание P (x): «Элемент х является работоспособным». Применяя это высказывание последовательно ко всем элементам множества X, получаем вектор логических переменных

X = [x₁, x₂, …, x_i, …, x_m, ],                   (8)

где         æистина, если   P (x_i ) – истинно;

      x_i =  í

            è  ложь, если   P (x_i ) – ложно.

Вектор Х может быть представлен в ЭВМ соответствующим массивом логических переменных размерностью m. Здесь уместно отметить аналогию в организации данных в программах и приведенных форм записи, так, выражение (7) соответствует отведению в ЭВМ m ячеек памяти, а выражение (8)—присвоению элементам массива конкретных значений. Многие алгоритмические языки программирования позволяют прямо оперировать с логическими переменными, однако программы часто оказываются более гибкими, если вместо логических переменных используют целочисленные индикаторы (9)

       æ1, если  P (x_i ) – истинно;