Инструкция: RAV = Р9; N = РО; В/О; С/П; РХ = D; С/П; РХ == Тср. При RAV = 0,5; N = 1000; Тср = 0,49641013; D =0,084913563, что дает e= 0,009214, по которой можно заключить, что полученное Тср лежит в области допустимых отклонений при данном N.
2.4. Имитационное моделирование функционирования системы.
Состояние СЭЭС достаточно полно представлено дискретными состояниями ее коммутационных элементов, некоторые из которых могут быть фиктивными и имитировать появление отказов. Как отказы, так и переключения, связанные с управлением структурой СЭЭС в аварийных и нормальных режимах, являются дискретными событиями, время появления которых подчиняется определенным статистическим законам. Поэтому, при статистическом моделировании определяется исходное состояние СЭЭС путем задания вектора индикаторов работоспособности элементов X, вектора управляющих воздействий Y и вектора состояния коммутационных элементов Z. Тогда функционирование СЭЭС можно представить в виде конечного автомата, описываемого рекуррентным выражением
ZP+1=Ф{XP, Yp, Zp),
где р—номер (индекс) текущего состояния автомата, который работает в «быстрой» тактности; и выходной функции работоспособности ФАЛ = Fs (X, Y, Z). Обычно
автомат должен организовать новую структуру СЭЭС за число тактов, не превосходящее заданное n. При моделировании автомат имитируется некоторым циклическим алгоритмом вычисления.
Рассмотрим простейший случай, когда отказы автомата не учитываются, вектор управляющего воздействия (заданный режим) Y фиксирован. Тогда интервалы между событиями в системе целиком определяется последовательностью отказов элементов СЭЭС. Для этого с помощью генератора псевдослучайных чисел с заданным законом распределения определяют моменты отказов всех элементов СЭЭС. Получается массив значения интервалов времени Т, который используется для определения последовательности отказов элементов (массив целых чисел ХС, представляющий случайную перестановку индексов элементов). Например, если система состоит из трех элементов, то исходное значение вектора Х записывается в виде массива Х=[1,1,1], допустим после последовательного определения отказов сформирован массив Т=[151, 626, 112], тогда массив будет иметь вид ХС = [3, 1, 2], что означает: первым откажет третий, вторым—первый и третьим—второй элементы.
После такой подготовительной работы нужно установить время отказа всей системы. Для этого последовательно вводят отказы с помощью выражения X[XC(i)]=0, где i—порядковый индекс массива ХС. Если i = 1, то Х[3] = 0,
Х= [1,1,0]. Теперь следует проверка условия работоспособности СЭЭС путем обращения к подпрограмме логической модели ФАЛ или конечного автомата. Подпрограмма может быть и полной динамической моделью, учитывающей броски токов, провалы напряжений, срабатывание защиты и т. д., но современные ЭВМ с последовательным выполнением операций пока не позволяют исследовать таким образом СЭЭС из-за неприемлемых затрат машинного времени.
Пусть в рассматриваемом примере ФАЛ имеет вид Fs=Х(1) [Х(2)vХ(3)]. Тогда ясно, что при первом отказе [Х(3)=0] получим Fs¹0. Это будет означать сохранение работоспособности системы. Следующий отказ делает Х[1]=0, теперь Fs=0. Фиксируется отказ СЭЭС, который в текущем эксперименте наступает в момент времени Ts=T[XC(i)] = 151, где i=2; XC(i)= 1.
Полученное таким образом Ts является результатом первого эксперимента и используется для вычисления Tcр, дисперсии D и стандарта ошибки e.
Результатом работы программы является распечатка в табличной форме зависимости
Rs(T), N, TS= Tcр, ERR=e.
Исходные данные вводят с клавиатуры пользователи по запросу программы.
2.5. Метод слоистой выборки (МСВ).
Методы прямой статистической имитации получили в научной литературе название методов Монте-Карло (ММК). При оценках надежности ошибка метода определяется выражением
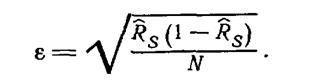
Так, при Rs = 0,891 и N = 100, e= 0,03116.
Для снижения дисперсии результатов имитационного эксперимента используют аналитико-статистические методы расчета Rs. Одним из таких методов является МСВ, иногда его называют методом «пропорциональной» выборки. Идея метода заключается в том, что все пространство состояний системы разбивается на слои (рис. 5) так, чтобы в слое дисперсия вероятностных мер была малой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.