Індивідуальний комплект навчально-методичних матеріалів з дисципліни "Надійність та технічна діагностика електрообладнання", страница 8

В каждом слое проводятся статистические испытания, причем число испытаний N_i в i-м слое пропорционально вкладу данного слоя в общую вероятностную меру R_s. В расчетах надежности индекс слоя определяется числом отказавших элементов в системе. Так, если СЭЭС состоит из m элементов, то основная аналитическая формула принимает вид:

	(12)

 

где А - живучесть, определяется статистически как вероятность отказа системы при отказе ровно i ее элементов, тогда дисперсия R_s определится из выражения

(13)

1,1

	Рис. 5   Номер слоя определяет число отказавших элементов системы.

 

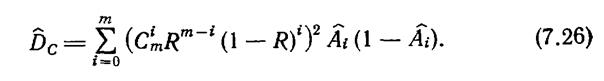
Пусть ФАЛ системы F = X₁(X₂ v Х₃). Вероятность безотказной работы

всех элементов одинакова R=0,9, тогда точное   аналитическое выражение дает

Rs=(2-R)R²=0,891.

При   использовании МСВ прежде всего проводят статистическую оценку условных вероятностей A_i. Непосредственно из ФАЛ видно, что A₀=1; A₁ = 2/3; А₂ = 0. Что позволяет определить точное значение дисперсии

D = (C¹₃ * 0,9(1 - 0,9))² * 2/3 (1 - 2/3);

D= 0,013122;

              

Видно, что по сравнению с МНК стандартную ошибку удалось понизить почти в 3 раза. Однако, при практическом использовании МСВ априори неизвестны A_i; и неизбежны бесполезные статистические испытания, например, во втором слое, в котором нет работоспособных состояний.

2.6. Метод звездной выборки (МЗВ).             ©

МЗВ разработан автором для расчета надежности проектируемых СЭЭС. МЗВ отличается от МСВ тем, что отказы назначаются не внутри слоя, а последовательно, т.е. «разрушаются» элемент за элементом, индекс i непрерывно возрастает до появления отказа СЭЭС. После чего эксперимент повторяется.

Алгоритм характеризуется следующей формулой вычислений:

,     

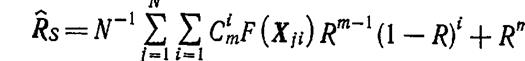где Х_ji — случайный вектор с мерой Хемминга H(X_ji) = m—i, отвечающий требованию: Н(X_ji-1 Å X_ji) = 1.

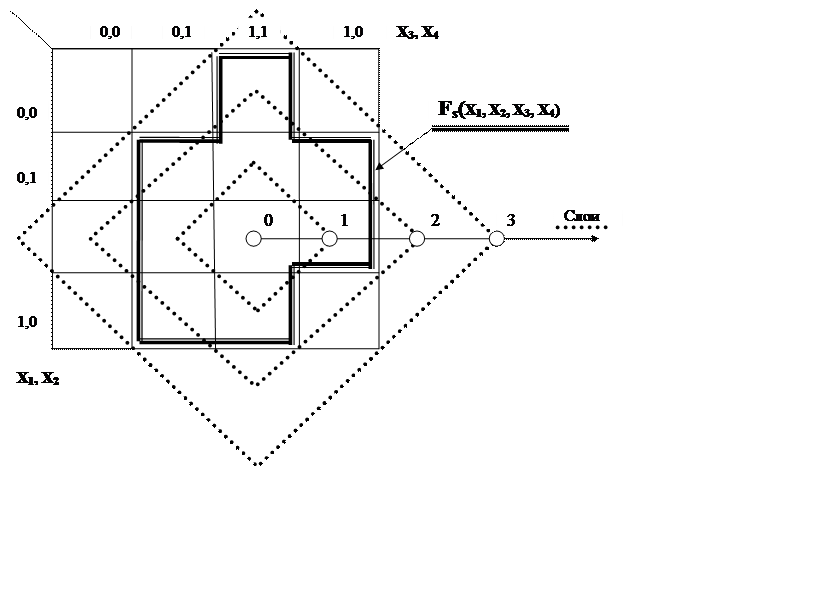
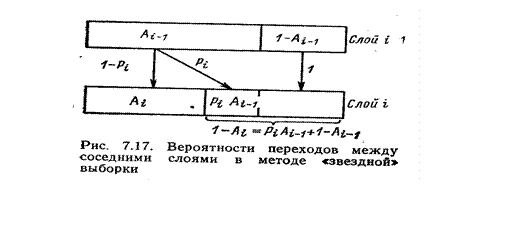
Преимущество метода в том, что он позволяет автоматически прекращать испытания при появлении значения ФАЛ F(X_ji)= 0. Испытания зависимы от слоев (рис. 5).

Рис.  6. 7.    7.

Действительно, вероятность попадания в зону исправного состояния i-гo слоя будет зависеть от вероятности такой же области в предыдущем слое

A_i=A_i-1,* (1-P_i), 1-А_i, = A_i-1 * P_i,

где P_i—вероятность перехода из исправного состояния в слое i-1 в неисправном слое i. Следовательно, дисперсия МЗВ в i-м слое определяется выражением

Dⁱ₃=[Cⁱ_mR^m-i(1-R)ⁱ]²A²_i-1P_i(1-P_i),

где P_i=(A_i-1 —A_i,)A_i-1, откуда полная дисперсия МЗВ

	из (13)

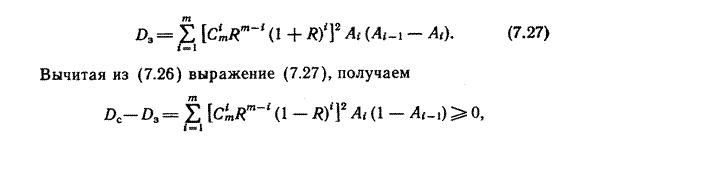
что доказывает большую точность МЗВ по сравнению с МСВ.

2.7. Метод распределенных параметров (МРП).     ©

(15)

       Излагаемый метод основан на представлении каждого элемента СЭЭС распределенными параметрами, т. е. элементы заменяются бесконечно большим количеством элементов, соединенных последовательно, но имеющих суммарную интенсивность отказов, равную интенсивности отказов исходного элемента. Но теперь выборка отказавших элементов проводится с «возвращением» т. е. на одной ветви схемы СЭЭС при проведении численного эксперимента возможно появление нескольких отказов. Расчетная формула

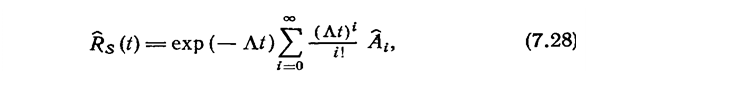
где 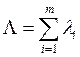 - суммарная интенсивность отказов; статистическая оценка вероятности отказа системы при появлении ровно i отказов микроэлементов.

Ошибка МКП оценивается дисперсией

(16)

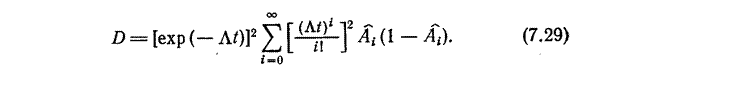
Программа отличается простотой организации, не требует формирования случайных перестановок и громоздких вычислений при статистическом эксперименте. Точность алгоритма близка к точности МЗВ. Недостатком является неопределенность длины массива A, который теоретически может стремиться к бесконечности, но практически на широком классе задач он был ограничен величиною 6m. Массив A может быть искусственно усечен, что соответствует ограниченному разложению R_s(t) в ряд.