Індивідуальний комплект навчально-методичних матеріалів з дисципліни "Надійність та технічна діагностика електрообладнання", страница 6

При X₀=0,5 получается множество случайных чисел Х={0,152545; 0,954155; 0,084227, ...}. Программа занимает малый объем памяти и ее можно без редактирования фрагментарно вставлять в другие программы.

Для получения генератора k случайных чисел с равновероятными исходами интервал (0...1) делится на k равных частей и организуется вывод на индикацию появления номера соответствующего подинтервала.

Программа 9/34. Генератор псевдослучайных событий с равномерными исходами.

Инструкция: k=P8; x₀=Р9; В/О; С/П; РХ = y₁; С/П; РХ = у₂, ..., С/П; РХ = у_n. В этой программе использована операция взятия целого от числа путем следующей подпрограммы

Инструкция: х = РХ; В/О; С/П; Int(х)= Р(х). При статистических испытаниях сложных систем возникает потребность в получении случайной перестановки К чисел, имитирующих случайную последовательность отказов элементов. С этой целью можно использовать алгоритм «перемешивания» массива.

Программа 10/34. Перемешивание массива чисел.

Инструкция: RАV=РД; x₁=Pl, ...; x_k = PK; K=PC; k = РХ; В/О; С/П; PI = x₁, ..., PK = x_k.

2.2. Генераторы псевдослучайных чисел с заданным законом распределения.

Эти генераторы используются для получения случайного времени безотказной работы элемента получают принимая случайное число RAV за вероятность безотказной работы RAV=R(t), откуда определяют t через обратную функцию R^-1(t).

Например, при экспоненциальном законе отказов

RAV = ехр (-lt); t=-1/l ln (RAV).

Программа 11/34. Генерация псевдослучайных чисел с экспоненциальным законом распределения.

Инструкция: RAV=P9; l=РА; В/О; С/П; t₁ = РХ; С/П; t₂ = РХ, ... .

Этот подход целесообразно использовать при простом виде обратной функции от R(t).

2.3. Статистические оценки числовых характеристик случайных величин.

           Поскольку всякие статистические оценки связаны с обработкой большого числа данных, очень важно использовать эффективные алгоритмы вычисления, некоторые из них приведены в данном разделе.

Оценка средней арифметической (математическое ожидание) выполняется согласно выражению

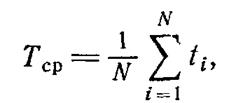
где t_i—значение времени безотказной работы і-го элемента;

N—число испытуемых элементов.

Стандартная ошибка при этом составит , где D- дисперсия.

Оценка дисперсии осуществляется по формуле

Программа 12/34. Проверка генератора псевдослучайных чисел.