Методичні вказівки до лабораторних занять з дисципліни «прикладна теорія цифрових автоматів», страница 4

Аналіз табл. 1.1 показує, що жодна двійкова комбінація в її рядках не повторюється. Отже, порівняння комбінації сигналів помилок у чотирьох контрольних розрядах із двійковими комбінаціями у рядках таблиці обов'язково забезпечить відкриття того розряду, в якому відбулася поодинока помилка.

Структура коду Хемінга для 15-розрядного числа (11 інформаційних розрядів та 4 контрольних) надана на рис. 1.1.

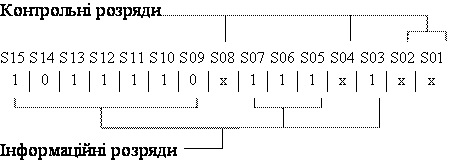
Рисунок 1.1  – Структура коду Хемінга для 15-розрядного числа

Узагальнені формули обчислення контрольних розрядів (4),...,(7) мають вигляд:

K4 = S09 + S10 + S11 + S12 + S13 + S14 + S15;                          (1.4)

K3 = S05 + S06 + S07 + S12 + S13 + S14 + S15;                          (1.5)

K2 = S03 + S06 + S07 + S10 + S11 + S14 + S15;                          (1.6)

K1 = S03 + S05 + S07 + S09 + S11 + S13 + S15,                          (1.7)

де + позначає суму по модулю 2 (mod 2).

Якщо деякі інформаційні розряди будуть відсутні (наприклад, S14, S15), то необхідно вважати, що вони дорівнюють нулю.

2.Код Хемінга з виправленням поодинокої помилки та контролем подвійної. Даний код відрізняється від коду з виправленням поодинокої помилки тим, що вводиться ще один додатковий контрольний розряд. Його називають «розрядом подвійного контролю» (ПК). Він визначається додаванням всіх розрядів (інформаційних та контрольних) по модулю 2, тобто по суті цей розряд подвійного контролю здійснює контроль на парність отриманого коду. Якщо уявити вектор помилки (ВП) коду Хемінга, як число, що приймає значення 0 або 1, то можна заповнити таку таблицю:

Таблиця 1.2 – Результати декодування в залежності від ПК та ВП