Методичні вказівки до лабораторних занять з дисципліни «прикладна теорія цифрових автоматів», страница 14

МКНФ   F(x₁,x₂, x₃,x₄) = .

На рис. 2.6 наведена КС для функції F(x₁,x₂, x₃,x₄) МДНФ у булевому базисі.

Рисунок 2.6 – МДНФ функції F(X₁,X₂, X₃,X₄)

Перехід від мінімальної диз’юнктивної нормальної форми до базиса Шефера простий: всі терми (логічні добутки) укладаються у дужки, а всі знаки диз’юнкції та кон’юнкції замінюють на операції Шефера (/). Якщо у МДНФ є однолітерний терм, то у базисі Шефера над ним ставиться заперечення.

Аналогічним чином виконується перехід від базиса Буля до базиса Пірса, якщо похідною формою є МКНФ.

При переході від МДНФ до базиса Пірса схема буде трьохступеневою та значення усіх змінних у порівнянні з ДНФ змінюються на інверсні. Нехай є функція:

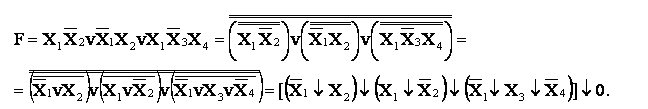
2.Синтезувати перетворювач чисел (0-9) з одного двійково-десяткового коду у інший (8421+3 ® 5121). Зобразимо цифри від 0 до 9 у відповідних кодах (табл. 2.1). Код 8421+3 буде визначати значення вхідних змінних, а код 5121 – значення вихідних змінних.

Таблиця 2.1 – Двійкови тетради кодів 8421+3 та 5121