Методичні вказівки до лабораторних занять з дисципліни «прикладна теорія цифрових автоматів», страница 22

Тригер S-типу – це тригер з двома входами R та S, що на відміну від тригера RS допускає наявність на входах комбінацій R=S=1. Завдяки пріоритету входу S тригери S-типу при R=S=1 з стану Q(t) переходять у стан Q (t+1) =1.

Повна та скорочена таблиці переходів наведені у табл. 3.1 та табл. 3.2. З повної таблиці переходів знаходимо допустимі комбінації сигналів на входах R та S для всіх чотирьох типів переходів Q (t) - Q (t+1) (табл. 3.3):

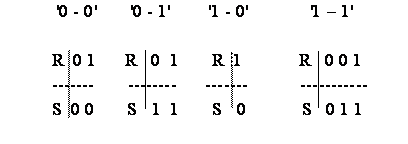
За можливими комбінаціями знаходимо шляхом склеювання кон’юнкцій, відповідних    можливим    комбінаціям,   відмітки   дуг    для   графа   переходів

S-тригера (рис. 3.2).

Для дуги, що виходить з а₀ та що входить до а₀(перехід: '0 – 0'), тобто петлі, отримаємо:`.

Для дуги з а₀ до а₁ (перехід '0-1'): .

Для дуги з а₁ до а₀ (перехід '1-0'): .

Для петлі з а₁ до а₁ (перехід '1-1'):`

.

Для складання матриці переходів S-тригера знайдемо взаємну залежність сигналів на входах R та S шляхом переходу до символічного запису та використовуючи формули розкладання булевих функцій на відповідних переходах:

Для переходу  '0-0'будемо мати: R = b₁; ;

для переходу  '0-1': R = b₂; =1;

для переходу  '1-0': R = 1; S = 0;

для переходу '1-1': R = b₃; ,

де b_1,  b_2, b_3,  b₄ – змінні, що приймають значення 0 або 1.

У підсумку одержуємо матрицю переходів S-тригера (таблиця 3.4).

Функція переходів тригера у момент t+1 може бути задана за допомогою карт Карно, що будуються по повній таблиці переходів тригера. Використовуючи карту Карно (рис. 3.3), можна побудувати мінімальну булеву функцію для опису функціонування S-тригера (характеристична функція переходів, рис. 3.6):