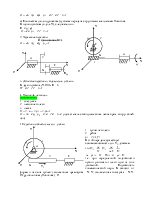
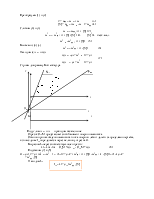
Построение планов ускорений. Кинематика зубчатых и фрикционных механизмов. Графический метод (метод Свердлова) определения передаточного механизма

Построение планов ускорений.

1.  Для построения планов ускорений должны быть построены планы скоростей.

2.1.Находим ускорение В₁₍₂₎.

2.2.Выбираем полюс плана ускорений (П).

2.3.Строим .

2.4.Определяем .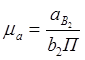

2.5.Записываем векторное уравнение для определения ускорения точки В₃.

        (1)

решаем (1) относительно

      (2)

анализируем уравнение (2)

Находим отрезок, который на плане ускорений будет изображать а_к.

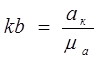
откладываем ускорение кариолиса на плане ускорений.

Откладываем следующие ускорения на плане ускорений

     //BD (к центру)

Находим отрезок, изображающий на плане ускорений

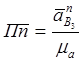
Откл. из П вектор

.

Проводим следующие ускорения .

2.6. Находим истинное значение .

2.7. Из уравнения (3) находим .

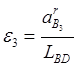
2.8. Находим направление углового ускорения 3-го звена. Для этого мысленно переносим вектор  в точку В.

2.9. Строим планы ускорений для других ускорений.

Кинематика зубчатых и фрикционных механизмов.

Особенностью этих механизмов является то, что все их звенья вращаются.

Т. е., для того, чтобы определить скорость точки, нужно знать его ω.

Для определения угловых скоростей в зубчатых и фрикционных механизмах вводится понятие передаточного отношения (U) и передаточного числа (i).

Под передаточным отношением i-го звена к j-му звену понимают отношение скорости ω_i  к ω_j, причем знак (+) берется в том случае. Если направления ω звеньев совпадают и (-), если нет.

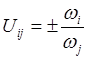            (1)

Под передаточным числом:

Пример:

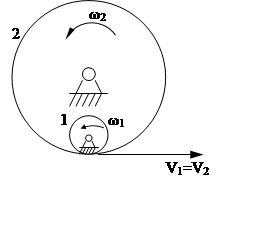
Меньшее из зубчатых колес называется шестерней.

.

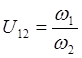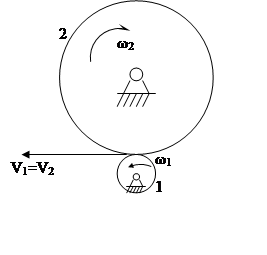
Если внутреннее зацепление , то U₁₂.

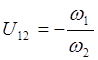
В зависимости от величины U_ij  механизмы разделяют:

- редуктор (уменьшает угловые скорости)

 - передача

 - мультипликатор

 - (плавно перем. вел.) вариатор

 - (ступ. перем. вел.) коробка скоростей (передач)

Выражение (определение) передаточного числа механизмов через параметры.

Из теоретической механики известно, что угловая скорость вращающихся звеньев

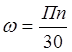  (2)

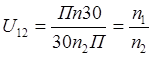
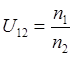
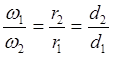 (3)

Найдем передаточное отношение через числа зубьев.

**********************

r_w – радиус начальной окружности

Начальными называются такие окружности, которые катятся друг по другу без скольжения.

p_w – шаг зубьев по начальной окружности.

z – число зубьев на колесе.

Длина начальной окружности определяется следующим образом:

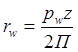           (4)

Подставим 4 в 3.

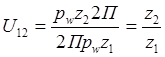
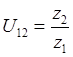
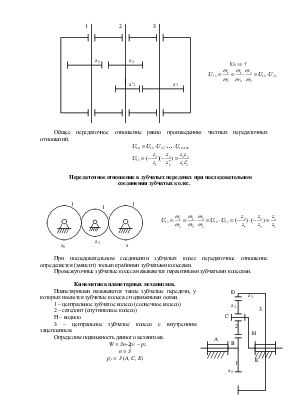
Передаточные отношения в зубчатых передачах с последовательно-параллельным соединением зубчатых колес.

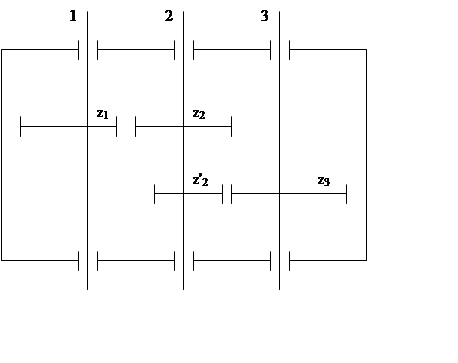
U_{1 3} = ?

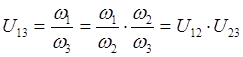
Общее передаточное отношение равно произведению частных передаточных отношений.

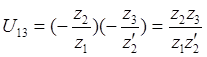
Передаточное отношение в зубчатых передачах при последовательном соединении зубчатых колес.

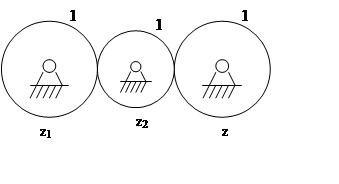
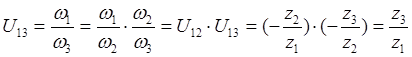
При последовательном соединении зубчатых колес передаточное отношение определяется (зависит) только крайними зубчатыми колесами.

Промежуточные зубчатые колеса называются паразитными зубчатыми колесами.

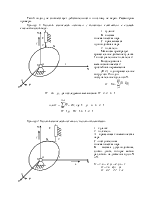
Кинематика планетарных механизмов.

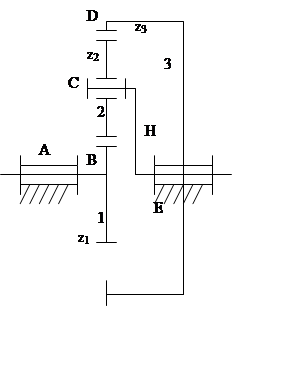
Планетарными называются такие зубчатые передачи, у которых имеются зубчатые колеса с подвижными осями.

1 – центральное зубчатое колесо (солнечное колесо)

2 – сателлит (спутниковое колесо)

Н – водило

3 – центральное зубчатое колесо с внутренним зацеплением.

Определим подвижность данного механизма.

W = 3n-2p₁ – p₂

n = 3

p₁ = 3 (A, C, E)

p₂ = 2(B, D)

W = 3·3-2·3-2 = 1

Передаточное отношение планетарных механизмов определяют графическим или аналитическим методом.

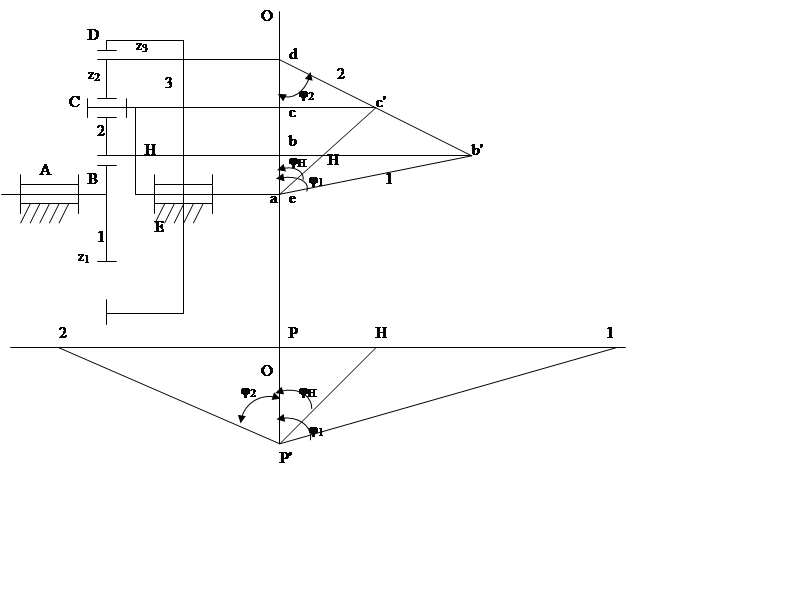Графический метод (метод Свердлова) определения передаточного механизма.

1.  Рисуем кинематическую схему исселдуемого планетарного механизма.

2.  Проводим структурный анализ механизма.

3.  Параллельно основанию механизма проводим нулевую линию.

4.  Проецируем все кинематические пары механизма на нулевую линию.

5.  Начинаем построение графика распр. линейных скоростей в звенья механизма.

V = ω_r

Построение графика линейных скоростей желательно начинать от водила (ω_н).

V_C = ω_н r_н.

Из точки С откладываем произвольной длины отрезок СС'.

Определяем масштабный коэффициент линейной скорости.

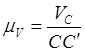
Соединив точку а с точкой С', получили график распред. линейных скоростей в звене Н.

Анализ схемы показал, что скорость точки D=0.

Соединив точки d и С', получим график распр. скоростей в звене 2.

Соединив точку a c b' – получим распр. скоростей в звене 1.

Получим график распр. линейных скоростей в зв. механизма.

Найдем: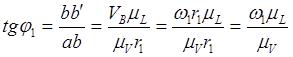

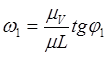
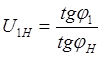
6.  Для определения передаточного отношения построим график изменения угловых скоростей.

Проведем линию .

Откл. произвольной длины отрезок РР'.

Переносим в точку Р' линии 1, 2 ….Н.

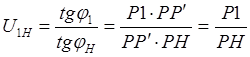
Для того, чтобы определить передаточное отношение в планетарной передаче между интервалами звеньев, необходимо найти соответствующее отношение между отрезками на плане угловых скоростей, причем, передаточное отношение будет положительным, если отрезки лежат по одну сторону от точки Р, и отрицательным, если отрезки лежат по разные стороны от точки Р.

Аналитический метод (метод Виллиса).

Идея метода Виллиса состоит в том, что всем звеньям планетарного механизма мысленно сообщается скорость – ω_н (в этом случае водило остановится).

- передаточное отношение звена 1 к звену Н. при неподвижном звене 3.

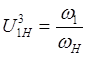
Запишем угловые скорости звеньев при остановленном водиле.

Найдем 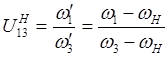      (1)