В соответствии с этой функцией получим два угла, для
того, чтобы определить который из углов является истинным, необходимо провести
дополнительный эксперимент: под любым из этих углов установим корректирующую
массу, раскр. станок, переводим его в режим выбега и фиксируем максимальную
амплитуду, если она значительно меньше, чем в первом испытании, то угол выбран
правильно, если амплитуда осталась большой, то корнем уравнения является другой
угол. Поэтому ![]() устанавливают под вторым углом и
эксперимент повторяют.
устанавливают под вторым углом и
эксперимент повторяют.
Балансировка гибких роторов.
Если валы прогибаются под воздействием установленных на них деталей и действующих на них сил называются гибкими.
Балансировкой гибких валов занимается теория колебаний.
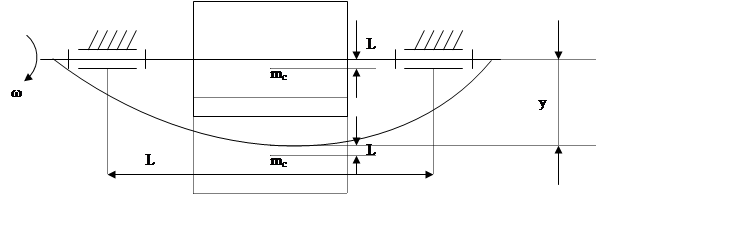 Рассмотрим
балансировку гибких вращающихся валов.
Рассмотрим
балансировку гибких вращающихся валов.
На вал будет действовать сила инерции.
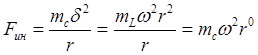 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Силу инерции уравновешивает сила упругости вала.
![]() (4)
(4)
с – коэффициент жесткости
![]()
![]()
решим последнее уравнение относительно y.
![]()
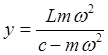
разделим числитель и знаменатель на ![]()
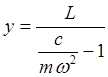
введем обозначение 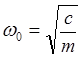 -
собственная частота вала.
-
собственная частота вала.
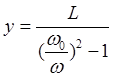 -
-
выражение для определения прогиба в гибком роторе, только для этого случая.
Проанализируем (5), для чего построим АЧХ.
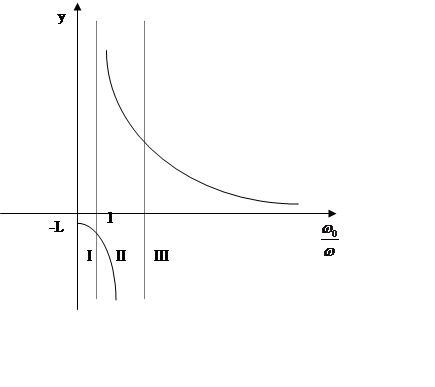
Балансировка заключается в уменьшении A до min.
I – дорезонансная зона
II – резонансная зона
III – зарезонансная зона
Чтобы отбалансировать вал, мы должны работать в I-ой и III-ей зонах. Для этого, чтобы не произошло разрушение машины в резонансной зоне, ее детали должны разгоняться как можно быстрее.
Для определения жесткости вала запишем формулу для его прогиба.
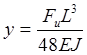 (6) – максимальный
прогиб.
(6) – максимальный
прогиб.
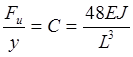
Уравновешивание плоских механизмов на фундаменте.
Все плоские звенья механизмов имеют m и движение с ускорением а, следовательно, на них действуют силы инерций. В соответствии с правилами механизмов, все действующие силы на механизм можно свести к одной силе, которая называется главный вектор сил инерции, а также к главному моменту всех сил инерции
![]() (1)
(1)
![]() (2)
(2)
Чтобы уравновесить машины на фундаменте, необходимо, чтобы эта сила и момент равнялись 0.
![]() (1*)
(1*)
![]() (2*)
(2*)
Различное статистическое уравновешивание машин и дин. или полное.
Статистическое проводится только по (1*), а динамическое по (1*) и (2*) одновременно. Так как динамическое уравновешивание явялется очень сложной задачей, то в М и М проводят только статистическое.
Статистическое уравновешивание машин производится за счет установки противовесов. Задачи статистического уравновешивания сводятся к определению mпр и rпр.
![]()
![]() , а это возможно при
, а это возможно при ![]() или
или ![]() , т.е.
ц.м. не подвижен.
, т.е.
ц.м. не подвижен.
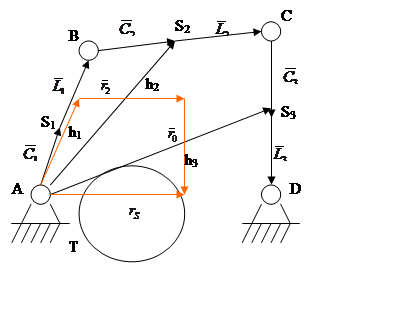 Рассмотрим,
как производится уравновешивание на фундаменте на примере шарнирного
четырехзвенника.
Рассмотрим,
как производится уравновешивание на фундаменте на примере шарнирного
четырехзвенника.
Заменим стороны векторами. В соответствии с теоретической механикой
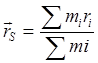 (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Подставим 2, 3, 4, 5 в (1)
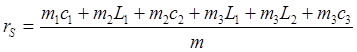 (6)
(6)
Перепишем (6) в следующем виде
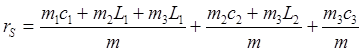 (7)
(7)
введем обозначения:
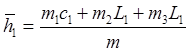 (8)
(8)
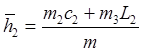 (9)
(9)
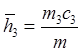 (10)
(10)
Отложим на схеме вектора h1 , h2 , h3
![]()
При вращении звеньев механизма центр масс будет перемещаться по каким-либо траекториям Т, следовательно механизм будет неуравновешен.
Чтобы центр масс был неподвижен, необходимо, чтобы векторный многоугольник h был подобен шарнирному четырехзвеннику.
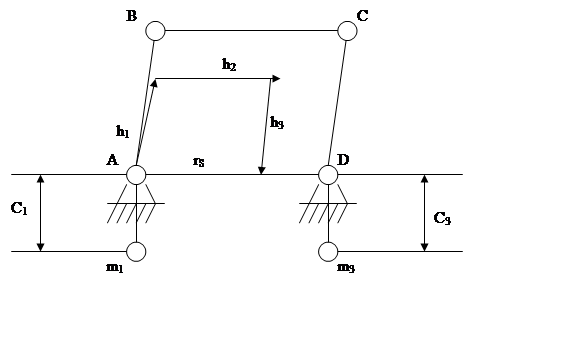
Запишем усл. подобия четырехзвенников.
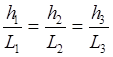 (12)
(12)
Из (12) можно записать 3 условия подобия, однако одно из них явялется вырожденным.
![]() (13)
(13)
![]() (14)
(14)
Раскроем 13 14, для чего подставим в них выражения 8, 9, 10.
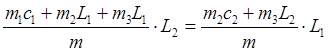 (15)
(15)
решим 15
относительно ![]()
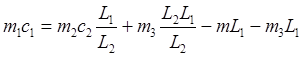
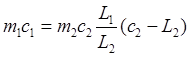 (16)
(16)
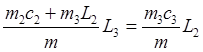 (17)
(17)
решаем 17
относительно ![]()
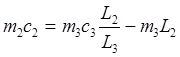
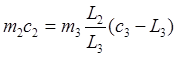 (18)
(18)
В уравнениях 16 и 18 неизвестными являются m1 , m2 , m3 , c1 , c2 , c3 .
Для того, чтобы уравновесить машины, необходимо задаться 4-мя величинами.
![]()
тогда из уравнений находятся m1 и m3.
?????????????
Для уравновешивания механизмов машин существуют конструктивные методы
??????????????
Синтез зубчатых передач.
Зубчатые передачи предназначены для передачи вращающего момента, с последующим его преобразованием из одной точки в другую.
Принцип действия с абсолютно жесткими звеньями основан на принципе бесконечного рычага.
Волновые зубчатые передачи или с гибкими звеньями используют принцип
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.