Исследуемый механизм имеет постоянную структуру, является сложным и однотипным. Он состоит из одного элементарного механизма и двух стационарных простых, которые имеют в своем составе только замкнутые кинематические цепи.
1.10. Определяем подвижность простых механизмов станка.
Анализ движений звеньев механизма и элементов кинематических пар показывает, что исследуемый сложный механизм, как и простые механизмы, существует в трех подвижном пространстве, в котором разрешены следующие простые независимые движения: два поступательных х и у вдоль соответствуещих осей; одно вращательное
![]() вокруг оси Z.
вокруг оси Z.
Подвижность элементарных механизмов определяется по формуле:
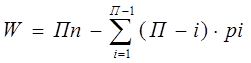
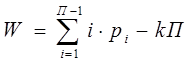 ,
где
,
гдеW-подвижность механизма;
П- подвижность пространства, в котором существует исследуемый механизм;
п- число подвижных звеньев механизма;
i- целочисленный индекс;
pi- число кинематических пар i-ой подвижности;
k- число независимых замкнутых контуров
Формулы для определения подвижности этих механизмов примут вид соответственно:
W=3n-2p1-p2 (1) (2) W=p1+2p2-3k , где k=р-n
Определим подвижность шарнирного четырех- звеника. Этот механизм имеет: три подвижных звена(n=3) 1,2,3; четыре (р=р1=4) одноподвижные кинематические пары A,B,C,O. Подвижность определяем по формуле (1)
Wш=3*3-2*4=1 и по формуле (2) k=4-3=1 Wш=4-3*1=1
Найдем подвижность кривошипно-ползунного механизма. Этот механизм имеет (n=3) подвижных звена 3,4,5 и четыре (р=р1=4) кинематические пары. Подвижность определяем по формуле(1)
Wк=3*3-2*4=1 и по ф-ле (2) k=4-3=1 Wк=4-3*1=1
1.11. Подвижность механизмов с незамкнутыми кинематическими цепями.
Т.к. в конвейере нет механизмов с незамкнутыми кинематическими цепями, то нет и необходимости определять их подвижность.
1.12. Определяем подвижность сложного механизма.
Подвижность комбинированного механизма определяется по формуле:
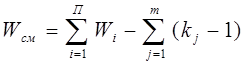 где
где
Wсм-подвижность сложного механизма;
i- индекс ,порядковый номер простого механизма;
Wi-подвижность i-го простого механизма;
n-общее число простых механизмов, входящих в состав сложного;
j- индекс общего звена;
т- суммарное число общих звеньев;
к –число присоединенных к j-му общему звену, простых механизмов. Подвижного сложного механизма строгального станка определяем по формуле(3)
Wсм=Wш+Wк-(к3-1)=1+1-(2-1)=1 ,где к3 определим в пункте 1.8.
Так как исследуемый сложный механизм является однотипным, его подвижность можно определить по формуле (1),(2) . Подставив в эти формулы исходные данные (n=5, p=p1=7) из пунктов 1.3. и 1.4 найдем подвижность этого сложного механизма
Wсм=3*5-2*7=1 k=7-5=2 W=7-2*3=1
Видно, что полученные результаты совпадают.
1.13. Проводим анализ структурный модели механизма станка. Проверяем, соответствует ли исследуемый механизм структурной математической модели.
Две равнозначные структурные, модели выглядят следующим образом:
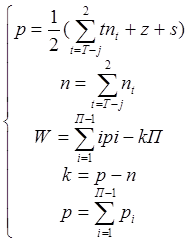
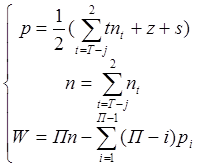 где
S-число присоединений стойке;
где
S-число присоединений стойке;
Z- число закреплении;
nt- число подвижных t-вершинных звеньев.
Исследуемый механизм имеет: семь (p=7)одноподвижных (p1=7) кинематических пар;
Пять(n=5)подвижных звеньев, из которых одно (n3=1), базовые (Т=3), трех вершинное(t=3) и четыре(n2=4)двухвершинных(t=2) три присоединения к стойке(S=3)и нет звеньев закрепления (Z=0).Подставив эти исходные данные в математическую структурную модель, получим:
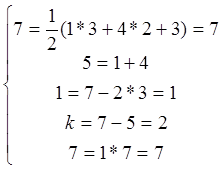
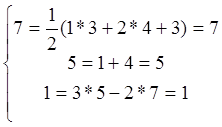
Так как уравнение модели превратились в тождества, то исследуемое устройство имеет правильную структуру и является механизмом.
1.14. Выделяем механизм первого класс.
В соответствии с классификацией механизм 1класса для исследуемого механизма совпадает с элементарным механизмом.
1.15. Выделяем структурную группу Ассура.
В механизме станка можно выделить следующие структурные группы:
 |
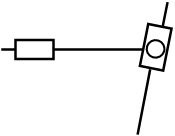 |
||||
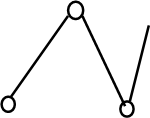 |
|||||
Видно, что структурные группы полностью подобны по видовому и составу звеньев и кинематических пар. Каждая из структурных групп имеет: два подвижных звена (n/=n/2=2), все звенья двухвершинные (t=2), базовое звено имеет две вершины(Т=2);три (р=3) одноподвижные (р1=3) кинематические пары, из которых две внешние (S/=2).
1.16. Проверяем, соответствует ли выделенные структурные группы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.