Построение планов ускорений. Кинематика зубчатых и фрикционных механизмов. Графический метод (метод Свердлова) определения передаточного механизма, страница 9

Запишем уравнение движения механизма в форме интеграла кинетической энергии:

                                     _j

J_ni *w_1i ² / 2 - J_1n0 * w₁₀² / 2 =ò  M_n * dj               (1)                                                        ^j0                     

w_1i =Ö   2 / J_ni *ò  M_n * dj  +    J_{1n 0} * w₁₀² / J_ni      (2)

w = w (j, t)      (3)

            Обычно интеграл, стоящий в (2) не выражается в квадратурах, то есть выражение (2) решается численным методом. В этом случае интеграл находится:

A_i+1= A_i + (M_ni + M_{n i+1}) * (j_{i +1} - j_i)/ 2

            Зная угловую скорость можно записать

w_1i = dj_1i / dt = w(j)

ò dj_I / w(j) = t + C₁                           (4)

            Если подинтегральная функция  решается непосредственно и в результате                     t = f(t)             (5).

            Если подинтегральная функция не решается в квадрантах, то решение аналогично, строя подинтегральную функцию. Перестраиваем (5) в виде j = f(t).

            Все эти рассуждения относятся только к случаюw₁₀ ¹ 0, то есть установ. режимом работы.

            Если исследуем режим разбега машины, то необходимо записать и исследовать уравнение движения машины в дифференциальной форме:

(w²_1i  / 2) * dJ_n / dj_I  + J_n * d²j₁ / dt²  =  M_n                         (6)

J_n = const, M_n = const

J_n * dj₁ / dt = M_n

w₁= M_n * t / J_n+ C₁                             (7)

            (7) можно представить

dj₁ / dt = M_n * t / J_n + C₁            (8)

            Интегрируя (8) получим

j₁ =M_n * t ² / 2 * J_n + C₁ * t  + С₂                               (9)

            С помощью (7) и (9) находится значение  w₁₀ ¹ 0 и j₁, а затем принимая новые   найденные значения за новые начальные условия интегрирования  уравнения движения механизма с помощью 1-го метода.

Графо – аналитический метод решения уравнений движения механизмов. Метод Виттенбауэра.

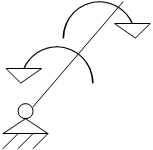   М_пс                           М_пс – момент приведенных сил сопротивления;

M_д                 J_n                                      М_д – момент движущих сил сопротивления;

М_п – приведенный момент;                         

                                                                                                                                                                                                                                                                                                               Решение исследуем на интервале 2p, в установившемся режиме:

t = 0; j_1i = j₁₀; w_1i = w₁₀;

при этом считаем, что M_д  =  const. Нахождение законов движения 1-го звена (звена приведения) просчитывают из диаграммы Виттенбауэра.

    T     

                 

J_n

 

Алгоритм решения.

1.  Находим для искомого механизма М_пс= f(j), J_пс = f(j)

2.  Строим график функции М_пс= f(j)

3.  Определяем масштабные коэффициенты:

m = М_пс /отрМ                  m _j = 2p / отрj

                                                                                                                                  _j

4.  Определяем момент движущих сил А_д = А_пс (за цикл): M_д * 2p = ò М_пс * dj

              ^j0

                                                                                                                 M_д  = ò М_пс * dj / 2p

5.  Находим изменение кинетической энергии на каждом шаге интегрирования

êT = T_i - T₀

 êT = êA

êT = êA_дв - êA _пс = ò М_д * dj - ò М_пс * dj

                        Строим зависимость êT = f(j)

6.  Строим повернутый на 90° график зависимости J_п = f(j)

7.  Определяем масштабный коэффициент m_j = J_пmax / отр J

8.  Строим диаграмму Виттенбауэра, для чего строим зависимость êT = f(J_п)

9.  Находим кинетическую энергию механизма в начальном положении

T₀ = J_п0 * w²₁₀ / 2

Находим отрезок, который будет изображать на графике отр T₀= T₀ / m_t

10. Откладываем от точки О вниз найденное значение отр T₀, обозначим эту точку                    О_т.

11.  Выберем поизвольную точку N и соединим ее с О_т.

12. Найдем tgy_N = nО_т / nN =  (êT + T₀) * m_J / m_t = w²_1N * m_J / 2 * m_t