Машиностроение \ Теория машин и механизмов

Построение планов ускорений. Кинематика зубчатых и фрикционных механизмов. Графический метод (метод Свердлова) определения передаточного механизма, страница 7

где     Т – кинетическая энергия механизма

qi – обобщенная  i-я координата

q¢i – обобщенная скорость i-ой обобщенной координаты

Qi, - обобщенная сила, имеет размерность [H]

            Уравнение движения зубчатого дифференциального механизма:

           

                        D                                                                                 W = 3 * n – 2 * p1 – p2 = 

              K                                           3                                                         3 * 4 – 2 * 4 – 2

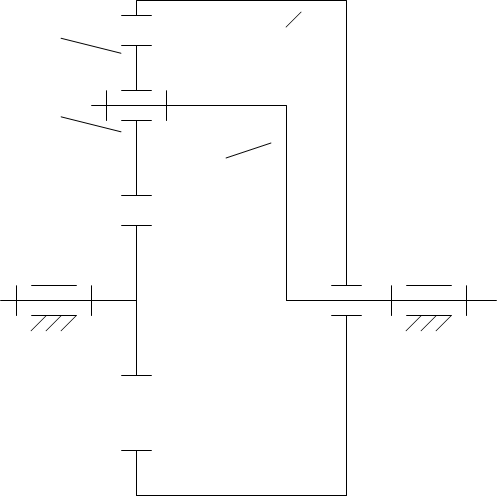
                 C                                                                                                    Пусть в зубчатой

              2                                                                                            дифференциальном ме -

                                                                                                            ханизме заданы парамет

                                                H                                                                 ры:

                        B

A                                                         E                 F                           J1, J2, J3 - моменты

                                                                        инерции всех звеньев,

       w1, w2, w3, wH,              

                                                                                                                                            m1, m2, m3, mH,                

                                                                                                                                                                                                        k

                                                                                  геометрические размеры

                                                                                       звеньев,

                                                                                                  M1, M2, MH - моменты

            Задача состоит в том, чтобы составить дифференциальное уравнение движения механизма.

            Так как механизм является дифференциальным, то для него запишем уравнение Лагранжа:

            d / dt  (¶T / ¶w1) - ¶T / ¶j1 = Mп1                                                

                                                                                    (1)

            d / dt  (¶T / ¶wH)- ¶T / ¶jH = MпH

Уравнение записано для 1-ой обобщенной координаты

            Запишем для кинетической энергии зубчатого дифференциального механизма:

T = J1 * w12 / 2 +k *  J2 * w22 / 2+ k * m2 * V22 / 2 + J3 * w32 / 2 + JH * wH 2 / 2       (2)

            Линейная скорость 2-го звена через wH:

V2 =w H * r H                          (3)

            Подставим (3) в (2):

T = J1 * w12 / 2 + k *  J2 * w22 / 2+ k * m2 *w2 H * r2 H / 2 + J3 * w32 / 2 + JH * wH 2 / 2         (4)

            Выразим угловую скорость 2-го и 3-го звена через угловые скорости 1-го звена и водила:

w2 = uH21 * w1 + u12H * wH          (5)

 

w3 = uH31 * w1 + u13H * wH           (6)

                   

Подставим (5) и (6) в (4):

2 * T = J1 * w12  + k *  J2 * (uH21 * w1 + u12H * wH) 2+ k * m2 *w2 H * r2 H +

+ J3 * ( uH31 * w1 + u13H * wH)2  + JH * wH 2    (7)

Раскроем скобки:

2 * T = J1 * w21  + k *  J2 * (uH21) 2* w21 + 2 * k * J2 * uH21 * u12H * w 1 * wH  +

 2 * k * J2 * ( u12H) 2  * w2H  + k * m2 *w2 H * r2 H + J3 * ( uH31 ) 2 * w21+ JH * wH 2 +

+ J3 * ( u13H ) 2 * w2H + 2 *  J3 * uH31 * u13H * w 3 * wH   (8)

            Введем следующие обозначения:

J 11 = J1+ k * J2 * ( u H21 ) 2  + J3 * (uH31 ) 2  - инерционный коэффициент 1-го звена        (9)

J 1H = k * J2 *  u H21* u 12H + J3 * uH31 * u13H - инерционный коэффициент H-го звена        (10)

J HH = JH+ k * JH * ( u 12H ) 2  + J3 * (u13H ) 2 + k * m2 * r2 H

            Подставим (9),(10),(11) в (8):

T =  1 / 2  [ J11 * w21  +  2 * J1H * w1 * wH + JHH  * wH 2 ]       (12)

            В соответствии с (1) найдем частные производные кинетической энергии:

Скачать файл