Пример 7. Объемный плоский кулачковый механизм с плоским толкателем и двухподвижной парой.
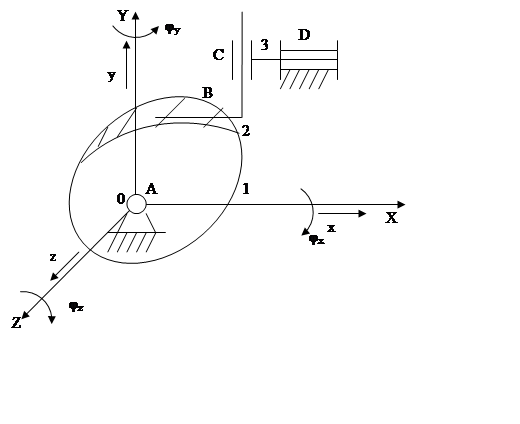1 – кулачок
2 – толкатель
3 – звено
n = 3, П = 6
p1 = 2(A, D), p2=1(С), p3 = 1(В)
W =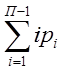 
-
kП, 
Подвижность механизмов, работающих на принципе зацепления.
Зубчатые передачи, наиболее распространенные в технике механизмы, это объясняется преимуществами: малыми габаритами, высоким КПД, большой надежностью в работе, постоянство передаточного отношения…
При формальном определении подвижности зубчатых механизмов считается, что высшая кинематическая пара всегда является двухподвижной. Зубчатый механизм в зависимости от вида его использования, считают то плоским, то пространственным, а червячную и коническую передачи представляют в виде другого условного механизма. Этот подход не верен, рассмотрим примеры.
Подвижность механизмов, работающих на принципе зацепления.
1. Конические (цилиндрические) зубчатые передачи.
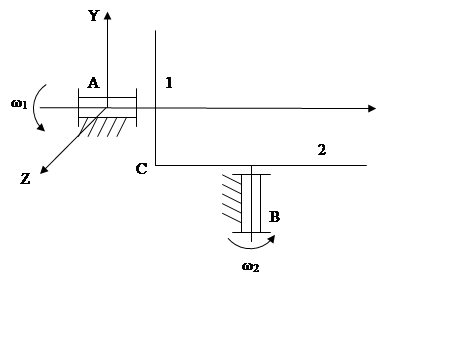Видно, что сов-ся 2 вращательных
движения, однако учтено должно быть только одно, так как другое является
зависимым.
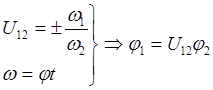
Таким образом, углы первого и второго звеньев взаимозависимы, что и требовалось доказать. Поэтому в качестве нез-го движения должно приниматься только одно перемещение любого из звеньев.
Элементы высшей кинематической пары В, в зависимости от угла наклона зубьев и их профиля, совершают относительно друг друга разное количество прост-их движений.
а) Прямозубая коническая (цилиндрическая) зубчатая передача с эвольвентным профилем зуба. В двухподвижна (вдоль X и Y), следовательно, механизм существует в П = 3 (x, y, φy).
W =3·2 – 2·2 –1=1б) Коническая
(цилиндрическая) зубчатая передача с непрямыми зубьями эвольвентного профиля. В
трехподвижна. (X,Y, Z)П = 4 (X,Y, Z, φy)
в) Коническая (цилиндрическая) зубчатая передача с круговым зацеплением Новикова.
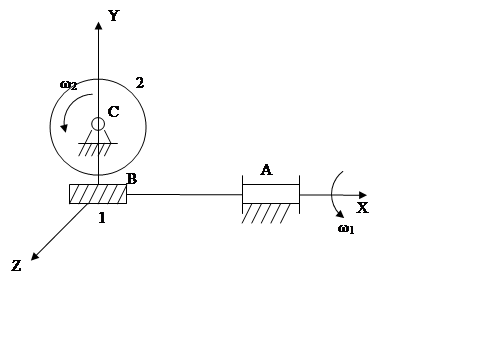В одноподвижная (вдоль Y),
следовательно П=2 (y, φ)
W = 2n –p1 = 2·2 – 3=1
2. Червячная передача.
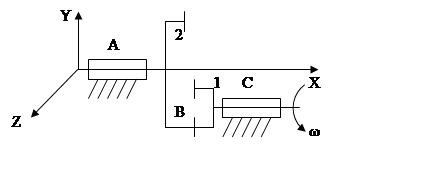
3. Зубчатая передача с торцовыми зубьями.
В двухподвижна (Y, Z) П = 3
4. Цевочный механизм.
************
1 – звездочка
2 – цевочное колесо
3 – цевка
П = 3, n = 3, p1 = 3, p2=1
5. Передача зубчатое колесо – рейка.
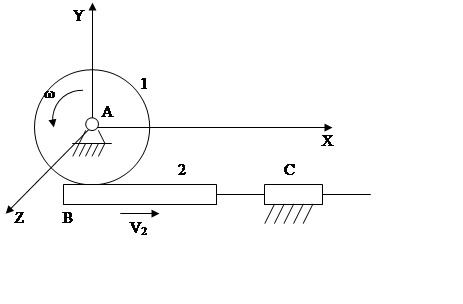
1 – зубчатое колесо
2 – рейка
p1 = 2 (А, С)
В этой передаче существует
взаимозависимость ω и V2, докажем
это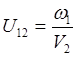
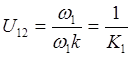
т.е. при определенной подвижности нужно учитывать только одно из этих движений. Подвижность кинематической пары В зависит от формы и наклона зубьев: эвольвентная прямозубая – X, Y; эвольвентная косозубая – X, Y, Z;круговинтовая (Новикова) –Z.
В зависимости от формы профиля зуба, передача зубное колесо-рейка будет существовать соответственно, в трех-, четырех- и двухподвижных пространствах. Однако во всех случаях W = 1.
Режимы работы машин и механизмов.
При работе машины различают три режима:
1. Разбег.
2. Установившийся.
3. Выбег.
Под установившимся режимом понимают такой режим машины, при котором скорость обобщенной координаты остается const или периодической функцией.
*****************
При реальной эксплуатации из-за налич. сущ. пр-ов установившегося режима не существует.
В режимах случайных колебаний всегда можно выделить такие периоды, когда сумма работ равна 0.
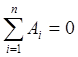
Этот режим и выб-ся за устан-ся, и называется квазиустановившимся.
Время между двумя ближайшими одноименными координатами в квазиустановившемся режиме называется период.
Для установившегося режима сумма элементарных работ всех внешних сил за период равна 0.
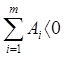- выбег
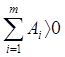- разбег
Режимы разбега и выбега называются неустановившимися.
КПД машины.
В любой машине происходит потеря энергии. В конечном итоге все потери превращаются в тепло и выделяются в пространство.
Для того, чтобы оценивать машины между собой вводят критерий.
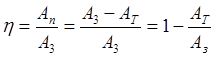
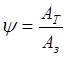- коэффициент
механических потерь
выясним пределы изменения φ и η
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.