![]() . (4.38)
. (4.38)
Расход в
русле площадью живого сечения ![]() составляет
составляет
![]() . (4.39)
. (4.39)
Зависимости (4.38) и (4.39) называют формулами Шези.
Формулы Шези могут служить для определения средней скорости в случае установившегося равномерного движения жидкости не только в безнапорных руслах, но и в трубах.
Следует учитывать, что формула применима только в случае квадратичной области сопротивления. Значения коэффициента С определяются по эмпирическим формулам, полученным в результате опытов с открытыми руслами и трубами.
Для удобства использования формул Шези вводят следующие обозначения:
![]() - модуль скорости, м/с;
- модуль скорости, м/с;
![]() - модуль расхода, м/с. (4.40)
- модуль расхода, м/с. (4.40)
С учетом выражений модулей скорости и расхода формулы Шези принимают вид:
![]() ;
;
![]() . (4.41)
. (4.41)
Гидравлические
потери напора по длине трубы получим из формулы Шези, где 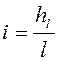 :
:
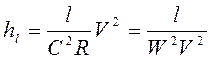 ; (4.42)
; (4.42)
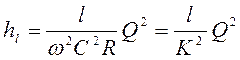 . (4.43)
. (4.43)
Удобно формулу потерь напора по длине для квадратичной области сопротивлений выразить через расход:
![]() ; (4.44)
; (4.44)
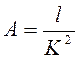 . (4.45)
. (4.45)
Параметр А получил название «удельное сопротивление».
Формула (4.44) называется трубопроводной формулой.
Трубопроводную
формулу можно получить, применив формулу Вейсбаха-Дарси (4.33), выразив
скорость через расход, - 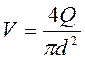 :
:
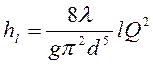 , (4-46)
, (4-46)
где
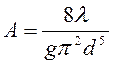 .
.
Используя
зависимости (4.44), (4.45) и (4.46), можно определить связь коэффициента Шези С
и коэффициента гидравлического трения ![]() , приняв
полное наполнение жидкостью трубы
, приняв
полное наполнение жидкостью трубы 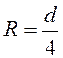 ,
, ![]() :
:
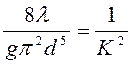 ;
; 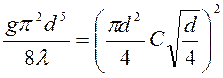 ,
,
откуда
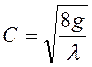 . (4.47)
. (4.47)
4.5. ЛАМИНАРНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ
ЖИДКОСТИ В КРУГЛЫХ ТРУБАХ
Ламинарное движение является упорядоченным слоистым течением без перемешивания частиц жидкости в потоке. При этом векторы скорости частиц будут параллельны оси потока, а поперечные скорости, перпендикулярные оси движения, отсутствуют. Так как движение имеет слоистый характер, то между слоями, которые движутся относительно друг друга, будут возникать силы внутреннего (вязкостного) трения и касательные напряжения. Движение жидкости подчиняется закону трения Ньютона.
Касательные напряжения при прямолинейном ламинарном движении согласно закону Ньютона
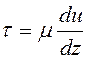 ,
,
где ![]() - градиент скорости.
- градиент скорости.
Рассмотрим
установившееся ламинарное движение вязкой жидкости в круглой цилиндрической
трубе радиусом ![]() (рис. 4.6). Так как
(рис. 4.6). Так как ![]() , то движение является равномерным. Будем
считать, что движущаяся жидкость в трубе разделяется на бесконечно большое
количество бесконечно малых по толщине концентрически располагающихся
цилиндрических слоев. Скорость в цилиндрическом слое, соприкасающемся со
стенками трубы, в результате его прилипания равна нулю.
, то движение является равномерным. Будем
считать, что движущаяся жидкость в трубе разделяется на бесконечно большое
количество бесконечно малых по толщине концентрически располагающихся
цилиндрических слоев. Скорость в цилиндрическом слое, соприкасающемся со
стенками трубы, в результате его прилипания равна нулю.
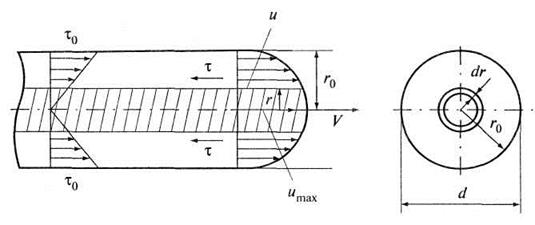
Рис. 4.6. К ламинарному движению жидкости в трубе
Касательные напряжения по поверхности рассматриваемого цилиндрического слоя толщиной dr
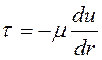 . (4.48)
. (4.48)
Знак
минус в (4.48) обусловлен тем, что скорость ![]() при
возрастании радиуса
при
возрастании радиуса ![]() убывает. Касательные напряжения
согласно основному уравнению равномерного движения в слое жидкости
убывает. Касательные напряжения
согласно основному уравнению равномерного движения в слое жидкости
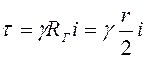 , (4.49)
, (4.49)
где ![]() - гидравлический радиус цилиндра
жидкости радиусом
- гидравлический радиус цилиндра
жидкости радиусом ![]() , выделяемый в трубе:
, выделяемый в трубе:
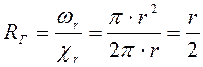 .
.
Подставляя выражение (4.49) в формулу Ньютона, получаем
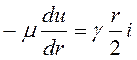 . (4.50)
. (4.50)
Приращение
скорости ![]()
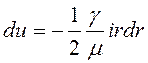 . (4.51)
. (4.51)
Интегрируя
дифференциальное уравнение и считая ![]() ,
, ![]() , найдем скорость
, найдем скорость
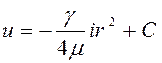 . (4.52)
. (4.52)
Постоянную
интегрирования С определим согласно условию, что у стенки трубы скорость
![]() при
при ![]() , тогда
, тогда
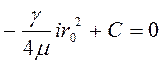 ,
,
откуда
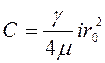 . (4.53)
. (4.53)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.