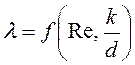Виды гидравлических сопротивлений. Режимы движения вязкой жидкости. Сопротивления при относительном движении твердого тела и жидкости, страница 11

.                                                     (4.90)

В зависимости от толщины вязкостного подслоя и пограничного слоя трубы можно разделить на гидравлически гладкие и шероховатые. В случае когда вязкостный подслой  больше шероховатости , т.е. все впадины и выступы погружены в подслой , такая поверхность стенки называется гидравлически гладкой.

Потери напора не будут зависеть от шероховатости: .

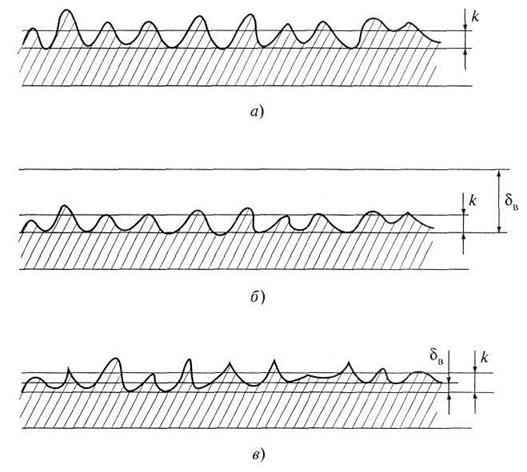
Рис. 4.12. Шероховатость стенки трубы:

а - абсолютная шероховатость ;

б - гидравлически гладкая поверхность стенки трубы;

в - шероховатая поверхность трубы

При условии  выступы выходят за пределы вязкостного подслоя и поверхность стенки является шероховатой.

Выступы, выходящие за подслой, способствуют активизации перемешивания частиц, возникновению вихреобразования в подслое и пограничном слое. Потери напора будут зависеть от относительной шероховатости трубы : .

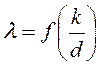При турбулентном движении коэффициент  определяется по эмпирическим формулам.

4 9 ПОТЕРИ НАПОРА ПО ДЛИНЕ ПРИ ТУРБУЛЕНТНОМ УСТАНОВИВШЕМСЯ РАВНОМЕРНОМ ДВИЖЕНИИ ЖИДКОСТИ

И.Никурадзе были проведены опыты по исследованию влияния шероховатости поверхности труб и числа Рейнольдса на потери напора по длине и на коэффициент гидравлического трения, т.е. 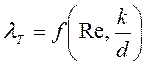. Опыты осуществлялись на гидравлическом стенде с круглыми трубами с искусственной однородной шероховатостью. Искусственная шероховатость создавалась путем наклеивания на внутреннюю поверхность труб песчинок одинакового размера. Относительные шероховатости в опытах были в пределах 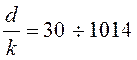. Эксперименты проводились как при ламинарном, так и при турбулентном режиме движения жидкости. Число Рейнольдса в экспериментах находилось в диапазоне . В трубах с разной относительной шероховатостью определялись потери напора по длине , при различных расходах. Коэффициенты гидравлического трения  вычислялись по формуле

.

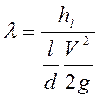По средней скорости V 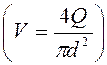 находилось число Рейнольдса 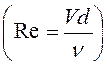. Результаты опытов были представлены в виде графиков, которые имели функциональную зависимость  с учетом относительной шероховатости в виде  (рис. 4.13). Величины  и Re - безразмерные.

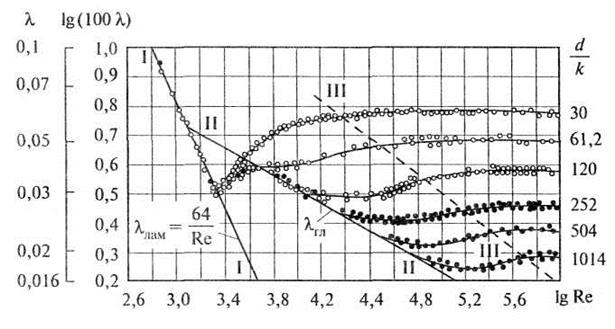
Рис. 4.13. График Никурадзе

На графике по оси ординат были отложены значения , а по оси абсцисс - величины . График позволил весьма наглядно показать влияние шероховатости трубы и числа Рейнольдса на коэффициент гидравлического трения и, соответственно, на потери напора по длине трубы.

На графике Никурадзе (см. рис. 4.13) можно выделить следующие характерные зоны ламинарного, неустойчивого и турбулентного режимов движения.

Ламинарная зона. В этой зоне полученные экспериментально величины  при разных относительных шероховатостях  легли на прямую I-I в левой стороне графика при значениях Re<2300 (=3,36), что соответствует ламинарному режиму движения. Таким образом, в данной зоне  не зависит от шероховатости труб, а зависит только от числа Re. Прямая линия I-I соответствует функции 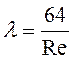, полученной теоретическим путем (см. п. 4.5, формула (4.68)).

Переходная (неустойчивая) зона. Эта зона соответствует переходу ламинарного движения в турбулентное и наоборот. На графике зона находится между линиями I-I и II-II при значениях числа Рейнольдса  (). Значение коэффициента  в этой зоне не зависит от шероховатости, .

Турбулентная зона. В турбулентной зоне имеется семейство кривых в зависимости от относительной шероховатости в виде . Начало кривых находится по линии II-II. Турбулентная зона разбивается на три области: гладкого сопротивления (гидравлически гладкие трубы), доквадратичного и квадратичного сопротивления (гидравлически шероховатые трубы).

Область гладкого сопротивления представляется на графике линией II-II при разных значениях  и числах Re. В этой области  не зависит от шероховатости а зависит только от числа Re, . Шероховатость внутренней поверхности труб не оказывает сопротивления движению жидкости при турбулентном режиме. Такие трубы называют гидравлически гладкими. В пределах этой области потери напора можно выразить зависимостью

.                                                          (4.91)