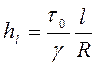 . (4.24)
. (4.24)
4.4. ПОТЕРИ НАПОРА ПО ДЛИНЕ ПРИ РАВНОМЕРНОМ УСТАНОВИВШЕМСЯ ДВИЖЕНИИ ЖИДКОСТИ
При равномерном установившемся движении жидкости в трубе средняя скорость и распределение скоростей по длине остаются неизменными. Следовательно, при определении потерь напора по длине можно использовать основное уравнение равномерного движения как при ламинарном, так и турбулентном движении в круглой трубе, выразив касательное напряжение на стенке формулой
![]() .
.
Для
круглой трубы диаметром ![]() гидравлический радиус
гидравлический радиус 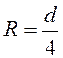 (
(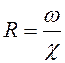 , площадь
живого сечения
, площадь
живого сечения 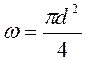 , смоченный периметр
, смоченный периметр ![]() ). Так как гидравлический уклон
). Так как гидравлический уклон 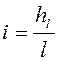 , то касательные напряжения на внутренней
поверхности трубы при движении вязкой жидкости будут равны
, то касательные напряжения на внутренней
поверхности трубы при движении вязкой жидкости будут равны
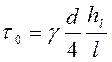 (4.25)
(4.25)
Опытами
было установлено, что сила сопротивления ![]() при
обтекании твердого тела вязкой жидкостью при установившемся движении зависит от
определенных параметров и эти сопротивления можно представить в виде следующей
функциональной зависимости:
при
обтекании твердого тела вязкой жидкостью при установившемся движении зависит от
определенных параметров и эти сопротивления можно представить в виде следующей
функциональной зависимости:
![]() , (4.26)
, (4.26)
где V - скорость набегающего потока жидкости; ![]() - плотность жидкости;
- плотность жидкости; ![]() - кинематическая вязкость;
- кинематическая вязкость; ![]() - характерный линейный размер тела;
- характерный линейный размер тела; ![]() - наибольшее сечение тела, которое
перпендикулярно вектору скорости
- наибольшее сечение тела, которое
перпендикулярно вектору скорости ![]() набегающего потока.
набегающего потока.
На основании анализов опытов и использования теории размерностей сила сопротивления может быть представлена следующей формулой:
![]() , (4.27)
, (4.27)
где b -
некоторый безразмерный коэффициент пропорциональности, называемый коэффициентом
сопротивления; ![]() - площадь тела.
- площадь тела.
Полагаем, что касательные напряжения, возникающие на поверхности тела, равны
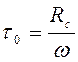 . (4.28)
. (4.28)
Тогда
![]() . (4.29)
. (4.29)
Воспользуемся полученной зависимостью для нахождения выражения по определению потерь напора по длине круглой трубы. Считаем, что касательные напряжения на поверхности трубы можно выразить зависимостью (4.29), V - средняя скорость в трубе.
Напишем равенство, используя формулы (4.25) и (4.29):
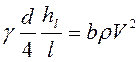 . (4.30)
. (4.30)
Потери напора по длине определим из равенства
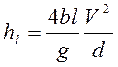 . (4.31)
. (4.31)
Умножив и разделив на 2 выражение (4.31), получим
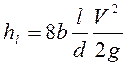 . (4.32)
. (4.32)
Обозначим
![]() ,
, ![]() - безразмерный
коэффициент, который получил название коэффициента гидравлического трения.
- безразмерный
коэффициент, который получил название коэффициента гидравлического трения.
Окончательная форма потерь напора по длине имеет следующий вид:
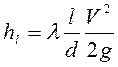 . (4.33)
. (4.33)
Формулу (4.33) принято называть формулой Вейсбаха-Дарси.
Учитывая уравнение равномерного движения в виде (4.24), коэффициент гидравлического трения можно выразить в виде
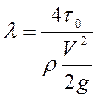 , (4-34)
, (4-34)
где 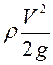 - динамическое давление.
- динамическое давление.
Коэффициент
![]() пропорционален отношению касательных
напряжений на стенке трубы к динамическому давлению, создаваемому потоком
жидкости. В общем случае коэффициент гидравлического трения
пропорционален отношению касательных
напряжений на стенке трубы к динамическому давлению, создаваемому потоком
жидкости. В общем случае коэффициент гидравлического трения ![]() зависит от режима движения (ламинарного
или турбулентного). На касательные напряжения на стенке
зависит от режима движения (ламинарного
или турбулентного). На касательные напряжения на стенке ![]() трубы
влияет шероховатость ее поверхности.
трубы
влияет шероховатость ее поверхности.
В случае безнапорного движения жидкости в различных руслах (каналы, канализационные и дренажные трубы) формула Вейсбаха-Дарси (4.33) не может быть применена. Для безнапорного установившегося равномерного турбулентного движения жидкости гидравлические потери по длине потока вычисляются по формуле Шези.
Для
вывода формулы Шези используем зависимости (4.23) и (4.29) для![]() . Напишем равенство
. Напишем равенство
![]() . (4.35)
. (4.35)
Средняя скорость в русле из (4.35)
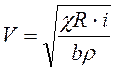 . (4.36)
. (4.36)
Или,
учитывая, что ![]() ,
,
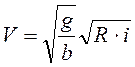 (4.37)
(4.37)
В
полученной зависимости обозначаем 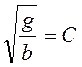 . Коэффициент С получил название коэффициента Шези.
. Коэффициент С получил название коэффициента Шези.
Средняя скорость при равномерном движении жидкости в русле
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.