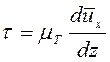Виды гидравлических сопротивлений. Режимы движения вязкой жидкости. Сопротивления при относительном движении твердого тела и жидкости, страница 10

.

4.8. ТУРБУЛЕНТНОЕ РАВНОМЕРНОЕ

ДВИЖЕНИЕ ЖИДКОСТИ В ТРУБАХ

В турбулентном потоке скорость движения частиц жидкости непосредственно у стенки трубы равна нулю. За счет вязкости жидкости на стенке трубы образуется тонкий заторможенный слой, который называется пограничным слоем, скорость на границе которого составляет 98-99% от скорости потока.

Пограничный слой  состоит из вязкого подслоя  и переходного слоя, находящегося между турбулентным ядром потока и подслоем (рис. 4.10).

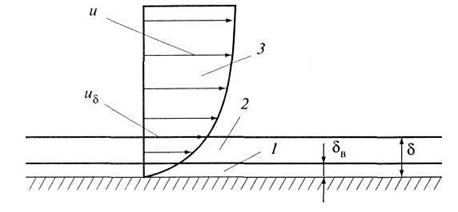
Рис. 4.10. Пограничный слой: 1 - вязкостный подслой; 2 - переходный слой; 3 - ядро

Внутри пограничного слоя может существовать как турбулентное, так и ламинарное движение в зависимости от числа Рейнольдса

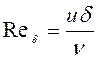,                                                          (4.88)

где  - скорость на внешней границе пограничного слоя.

В турбулентном ядре в результате интенсивного перемешивания и пульсаций скоростей частиц жидкости распределение скоростей по живому сечению потока более ровное по сравнению с ламинарным режимом движения. Движение в ядре практически не зависит от вязкости, градиент скорости  близок к нулю, и можно полагать, что оно практически соответствует движению идеальной жидкости. Как показали опыты, отношение средней скорости V к максимальной  по центру трубы находится в пределах 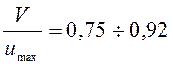. Отношение скоростей возрастает с увеличением числа Рейнольдса (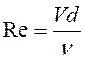), при этом на отношение влияет шероховатость стенок трубы (рис. 4.11).

Теоретически и подверждено результатами опытов в трубах, что местная скорость  соответствует средней скорости V в точке, находящейся на расстоянии  от стенки трубы.

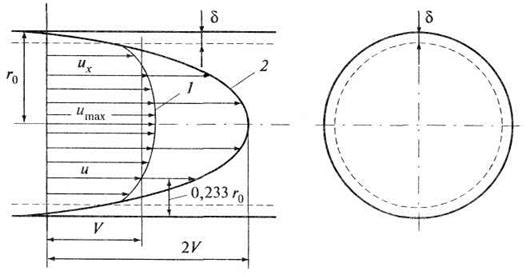
Рис. 4.11. Распределение скоростей в круглой трубе:

1 - эпюра скоростей при турбулентном движении;

2 - эпюра скоростей при ламинарном движении

Следует отметить, что коэффициент неравномерности распределения скоростей в трубе при турбулентном движении , тогда как при ламинарном движении . При решении различных гидравлических задач в случае турбулентного режима движения принимается .

Толщина подслоя, полученная теоретическим путем,

.

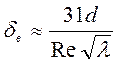Таким образом, толщина вязкостного подслоя зависит от диаметра, числа Рейнольдса и коэффициента гидравлического сопротивления .

Проведенные исследования показали, что шероховатость внутренней поверхности труб влияет на распределение скоростей в живом сечении потока жидкости и на потери напора по длине.

Трубы изготавливаются из различных материалов (сталь, чугун, бетон, стекло, полимеры и т.д.). Способ изготовления и вид материала влияют на шероховатость трубы. Шероховатость определяется высотой выступов и неровностей на поверхности стенок труб. С течением времени на поверхности труб появляются ржавчина, коррозия, отложение солей и осадков, что также будет влиять на шероховатость.

Характеристикой, выражающей шероховатость, служит средняя высота выступов и неровностей. Такая средняя высота, выраженная в единицах длины, называется абсолютной шероховатостью и обозначается буквой . Фактически шероховатость поверхности неоднородна по длине труб. На распределение скоростей и потери напора влияет диаметр трубы при одинаковой абсолютной шероховатости. Поэтому для определения этого влияния шероховатости и диаметра d введено понятие относительной шероховатости трубы  (рис. 4.12).

Как показали опыты с трубами, на потери напора влияет не только средняя высота выступов , но и степень, форма, густота и характер их расположения. Для упрощения влияния этих обстоятельств было введено представление об эквивалентной шероховатости . Эквивалентной шероховатостью называется высота выступов песчинок одинакового размера, при которой коэффициент гидравлического трения  соответствует действительной естественной шероховатости трубы. Относительная эквивалентная шероховатость - .

На основании вышеизложенного можно считать, что при турбулентном движении потери напора по длине могут зависеть как от числа Рейнольдса Re, так и от относительной эквивалентной шероховатости .

Коэффициент гидравлического трения можно выразить в функциональном виде: