Виды гидравлических сопротивлений. Режимы движения вязкой жидкости. Сопротивления при относительном движении твердого тела и жидкости, страница 3

Как было установлено опытами, вполне развитое турбулентное движение имеет место при . Это значение можно принять за , при котором средняя скорость будет соответствовать верхней критической скорости  (). При  будет неустойчивый (неупорядоченный) режим движения, т.е. переходная неустойчивая критическая область течения жидкости.

Число Рейнольдса, являясь безразмерной величиной, одинаково для всех жидкостей и газов, а также диаметров трубопроводов. Однако для разных жидкостей и газов будут иметь место соответствующие критические скорости. В случае одинаковых диаметров труб и разных жидкостей критические скорости пропорциональны кинематическим вязкостям

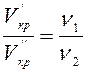.                                                              (4.4)

Таким образом, при определении режима движения жидкости в трубопроводе необходимо знать его диаметр, вязкость жидкости и среднюю скорость. Вычислив число Рейнольдса, сравнивают его с критическими значениями  и .

Экспериментами, проведенными Рейнольдсом, а также многочисленными данными, полученными разными учеными, было установлено, что гидравлические потери напора  по длине трубы зависят от средней скорости , т.е. от режима движения. Опытным путем была определена зависимость . Опыты заключались в следующем. На трубе диаметром  в сечениях 1-1 и 2-2 размещались пьезометры на участке длиной  (рис. 4.3). Устанавливая в трубе разные расходы, находилась средняя скорость 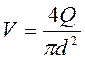 и измерялись показания пьезометров в сечениях , .

Разность показаний пьезометров - потери напора по длине

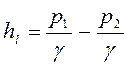.                                                       (4.5)

На основании опытных данных был построен график  (рис. 4.4), на котором нанесены значения критических скоростей и . На графике можно отметить следующие зоны. В зоне а при средней скорости  (ламинарный режим) потери напора в трубе прямо пропорциональны скорости :

.                                                              (4.6)

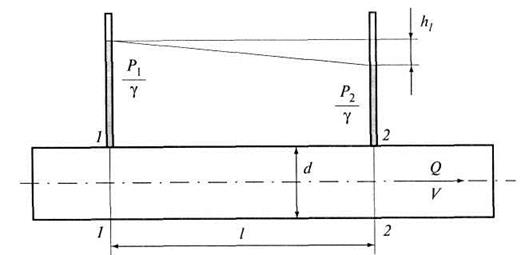
Рис. 4.3. Определение потерь напора по длине трубы

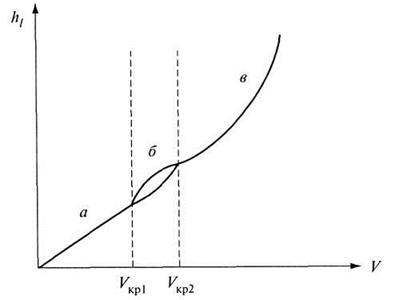
Рис. 4.4. Зависимость потерь напора по длине от скорости

В зоне в, где  (турбулентный режим движения), потери напора выражаются параболической функцией

,                                                             (4.7)

где  - некоторый размерный коэффициент;  - показатель степени.

В зоне в показатель степени с увеличением скорости изменялся от 1,75 до 2.

Между ламинарной и турбулентной зонами находится зона б неустойчивого движения, где . В этой области струйчатое движение нарушается, как и неустойчиво гидравлическое сопротивление.

За интервал времени может наблюдаться как упорядоченное (струйчатое) движение, так и беспорядочное, т.е. в этой области жидкость находится в промежуточном неустойчивом состоянии. В этой зоне не удалось получить функциональную зависимость .

Для турбулентного движения при больших скоростях и числах Рейнольдса показатель степени . Это область квадратичного сопротивления:

.                                                             (4.8)

Коэффициент В учитывает размеры трубы и ее внутреннюю шероховатость поверхности, вид жидкости, ее плотность и вязкость.

При показателе степени в пределах  движение жидкости будет происходить в области доквадратичного сопротивления.

♦ Пример 4.1

Определить критическую скорость, отвечающую переходу от ламинарного режима движения к турбулентному, для трубопровода диаметром мм при движении в нем воды, минерального масла и воздуха при их температуре 20°.

По таблице П 1.3 приложения находим кинематическую вязкость веществ:

вода -                             м²/с;

минеральное масло -  м²/с;

воздух -                         м²/с

Считаем, что переход от ламинарного режима движения к турбулентному происходит при .

, .

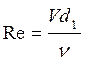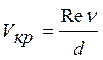Для воды 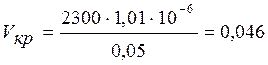 м/с.

Для масла 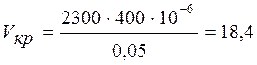 м/с.

Для воздуха 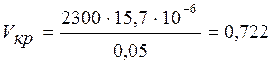 м/с.

4.3. ОСНОВНОЕ УРАВНЕНИЕ УСТАНОВИВШЕГОСЯ РАВНОМЕРНОГО ДВИЖЕНИЯ ЖИДКОСТИ

Рассмотрим равномерное установившееся движение потока конечных размеров, произвольной формы, наклоненного под углом  к горизонту. При равномерном движении средние скорости , живые сечения по длине потока постоянны.