Виды гидравлических сопротивлений. Режимы движения вязкой жидкости. Сопротивления при относительном движении твердого тела и жидкости, страница 4

Выделим в потоке участок между сечениями 1-1 и 2-2 длиной  (рис. 4.5).

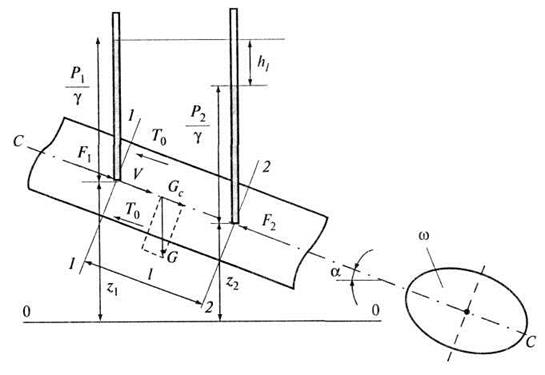
Рис. 4.5. К выводу уравнения равномерного движения

Ось С-С, относительно которой будем рассматривать внешние силы, действующие на объем жидкости между выбранными сечениями, проходит по оси потока. При равномерном движении потока скорости в сечениях по длине постоянны, . Написав уравнение Бернулли для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, получим, что потери напора по длине на участке длиной

.

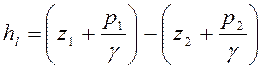Определим все внешние силы, действующие на участок потока между сечениями 1-1 и 2-2.

1.  Сила тяжести участка

,                                                              (4.10)

где  - удельный вес жидкости;  - площадь живого сечения.

Сила тяжести G приложена в центре тяжести участка и направлена вертикально вниз.

Проекция силы тяжести на ось С-С

,                                                    (4.11)

где  - угол наклона оси С-С к горизонту.

Из рис. 4.5 видно, что разность

.                                                 (4.12)

Тогда

.                                               (4.13)

2.  Силы давления.

При равномерном плавно изменяющемся движении гидростатическое давление  в разных точках плоского живого сечения постоянно. Силы давления  и  в сечениях 1-1 и 2-2 нормальны к этим сечениям. Сила  направлена в сторону движения потока, сила  - в обратную сторону:

;                                             (4.14)

где ,  - давления в центре тяжести живых сечений 1-1 и 2-2.

3.  Силы сопротивления движению.

Сила сопротивления - сила трения, возникающая при движении вязкой жидкости. Сила сопротивления , приложенная вдоль боковой поверхности стенок участка, направлена в сторону, противоположную движению потока, и называется силой внешнего трения. Кроме силы внешнего трения, возникающей на стенке, существуют силы внутреннего трения Т. При рассмотрении движения струек жидкости между ними возникают силы трения. Для струйки, движущейся с большой скоростью, сила трения направлена в обратную сторону ее движения, а для другой струйки с меньшей скоростью сила трения будет направлена в сторону движения. Эти силы парные и равны друг другу. В связи с этим сумму сил внутреннего трения во всех струйках потока жидкости можно считать .

На стенке участка возникают касательные напряжения  в результате трения между стенками русла (потока конечных размеров) и жидкостью.

Значение силы сопротивления

,                                                        (4.15)

где  - длина контура живого сечения, соприкасающегося со стенкой потока конечных размеров, - смоченный периметр;  - площадь боковой поверхности участка жидкости.

Так как движение жидкости равномерное, то ускорение выделенной массы участка равно нулю. Можно считать что все внешние силы, приложенные к участку потока жидкости между сечениями 1-1 и 2-2, находятся в равновесии.

Сумма проекций всех внешних сил на ось С-С равна нулю, т.е.

.                                         (4.16)

Подставим в (4.16) выражения (4.13), (4.14) и (4.15), тогда уравнение равновесия приобретает следующий вид:

.                 (4.17)

Разделим выражение (4.17) на , получим

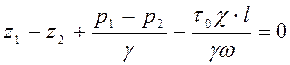.                           (4.18)

или

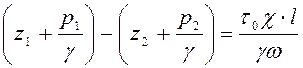.                         (4.19)

Подставив полученное выражение (4.19) в (4.9), получим зависимость потерь напора

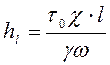.                                                         (4.20)

Введем в формулу (4.20) гидравлический радиус 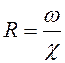. Тогда уравнение потерь напора по длине (4.20) примет вид

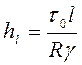                                                              (4.21)

Разделив уравнение (4.21) на длину участка , будем иметь

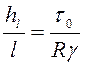.                                                            (4.22)

Отношение 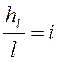 - гидравлический уклон.

Уравнение (4.22) представим в следующем виде:

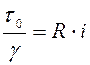.                                                            (4.23)

Полученное уравнение (4.23) называется основным уравнением установившегося равномерного движения. Это уравнение можно применить как для ламинарного, так и для турбулентного движения. Потери напора по длине при равномерном движении потока жидкости конечных размеров любой формы