Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи. Помехоустойчивость и пороговые свойства цифровых систем передачи непрерывных сообщений, страница 9

В общем случае при использовании многоосновного кода вследствие действия помех может произойти ошибка в любом разряде. Учитывая, что любое число при многоосновном коде можно записать в виде суммы (3.18), аномальную ошибку, выраженную числом шагов квантования при равномерном распределении сообщения, можно представить в виде

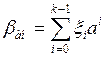
В этой формуле а — основание кода,— разрядная цифра, кото­рая представляет собой случайную величину, принимающую одно из следующих значений: если символ принят верно, то  = 0, если до­пущена ошибка, томожет принимать значения от ±1 до ±(а — 1).

Считая ошибки в разрядах независимыми и учитывая, что диспер­сия суммы случайных величин равна сумме дисперсий отдельных со­ставляющих, выражение для дисперсии аномальной ошибки, выражен­ной числом шагов квантования, будет иметь вид

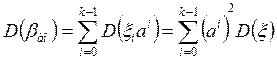.                 (6.27)

где D () — дисперсия случайной величины, одинаковая для всех разрядов.

Поскольку число единиц и нулей в среднем во всех кодовых словах можно приближенно считать одинаковым и все кодовые слова предпо­лагаются при передаче равновероятными, то распределение ошибок в симметричном канале оказывается симметричным и средняя ошибка будет равна нулю. Дисперсия случайной величины £ определяется за­висимостью

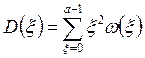                                       (6.28)                         

В этой формуле w () = р() — распределение вероятностей зна­чений ; р() — вероятность трансформации одних элементарных сиг­налов в други .

Если все уровни передаваемого сообщения равновероятны и все элементарные символы передаются с одинаковой помехоустойчивостью, то [см. формулу (5.64)]

                                  (6.29)

Подставляя выражения (6.28) и (6.29) в (6.27), получим

                                 .

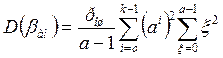Учитывая, что сумма возрастающей геометрической прогрессии со знаменателем a²

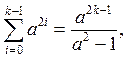
а сумма конечного числового ряда

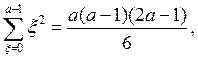
окончательно имеем

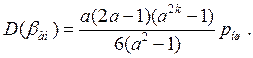                  (6.30)

Дисперсия аномальной ошибки, выраженная в единицах передава­емого сообщения,

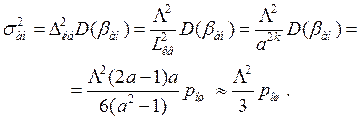    (6.31)

Дисперсия погрешности, приведенная к дисперсии гауссовского со­общения,

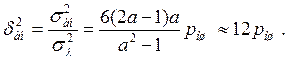          (6.32)

При a = 2 второе приближение будет точным.

Из полученного приближенного выражения видно, что дисперсия аномальной погрешности зависит лишь от вероятности ошибки в эле­ментарном символе р_ош. Строго говоря, выражения (6.31) и (6.32) по­лучены для равномерного распределения сообщения. Однако можно по­казать, что при достаточно высоких требованиях к точности передачи закон распределения  ω(λ) несущественно влияет на .

Оценка аномальных погрешностей при ДИКМ. Строгий расчет ано­мальных погрешностей в цифровых системах передачи с ДИКМ с уче­том размножения и накопления аномальных погрешностей встречает ряд математических трудностей. Поэтому здесь будет дана лишь при­ближенная оценка р_анр и  в системах с ДИКМ без учета размноже­ния аномальных погрешностей. Напомним, что процесс накопления и размножения аномальных погрешностей в системах передачи с ДИКМ состоит в том, что ошибочный прием одной кодовой комбинации ведет к искажению не только данного отсчета (координаты) сообщения, но и ряда последующих отсчетов, поскольку предсказанные значения очередного отсчета на передающей и приемной сторонах будут отли­чаться. Существуют различные способы уменьшения влияния этого эффекта (см. § 2.6).

При указанном допущении для расчета р_анр и δ_анр может быть ис­пользована изложенная методика расчета при ИКМ с учетом того, что динамический диапазон изменения конечных разностей Λ_р и число раз­рядов в кодовой комбинации k_р будут своими и менее соответствующих значений при ИКМ. Тогда в соответствии с выражениями (6.26) и (6.32) будем иметь:

                         (6.33)

                       (6.34)

Из сопоставления выражений (6.26) и (6.33), (6.32) и (6.34) видно, что при одинаковом качестве канала передачи, определяемом р_ош, в системе с ДИКМ обеспечивается в  раз меньшее значение приведен­ной дисперсии аномальной погрешности и в k_p/k раз меньшее зна­чение p_анр чем в системе передачи с ИКМ.