6.2 Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи
Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи в общем случае зависят от многих факторов: метода модуляции и ее широкополосности, метода приема (метода обработки сигнала в приемном устройстве, вида помех и их статистических характеристик) вида сообщения и его статистических характеристик, отношения сигнал-помеха на входе приемника, требований к качеству передачи сообщения.
Вполне естественно, что охватить все возможное многообразие рассматриваемых систем передачи и условий их использования не представляется возможным. Поэтому в данном параграфе основное внимание будет уделено рассмотрению аналоговых непрерывных систем передачи с частотной модуляцией при двух наиболее распространенных методах приема (стандартном и синхронно-фазовом) в условиях воздействия белых гауссовских помех. Затем будет дана краткая сравнительная оценка помехоустойчивости таких систем передачи с другими видами модуляции и при воздействии других видов помех.
Механизм воздействия флуктуационной помехи. Упрощенное представление о характере воздействия флуктуационных помех на гармонический сигнал дает векторная диаграмма (Рисунок 6.2, а).На этой диаграмме изображена сумма немодулированного гармонического сигнала (несущей)
![]()
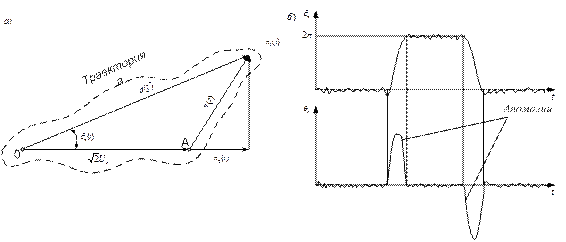
Рисунок 6.2
и узкополосной гауссовской флуктуационной помехи (на выходе полосового фильтра), которую можно представить в виде
![]()
где n1(t) и n2(t) — независимые квадратурные стационарные гауссовские процессы с той же, что у n(t), спектральной плотностью мощности N0 (см. § 2.2).
Выражение для результирующего вектора суммы сигнала и помехи будет иметь вид (при φ0 = 0)
![]() (6.2)
(6.2)
где
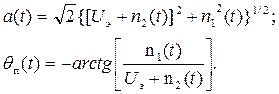
На рисунке 6.2 изображено относительное расположение неподвижных векторов и осей (в момент t = 0), при этом предполагается, что оси координат вращаются с угловой скоростью ω0.
При большом значении отношения сигнал-помеха [когда n1(t) и n2(t) по сравнению с Uэ малы] большую часть времени имеем:
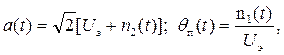 (6.3)
(6.3)
которые являются случайными процессами.
Вследствие воздействия помехи на полезный сигнал результирующий вектор y(t) будет флуктуировать по амплитуде и фазе, т. е. будут возникать искажения при использовании как AM так и УМ сигналов. Распределение вероятностей для a(t) и θп(t) в общем случае зависит от отношения сигнал-помеха.
При большой помехе имеем:
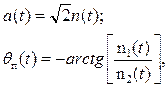
т. е. амплитуда и фаза сигнала
будут определяться лишь помехой. Это означает, что в некоторые интервалы
времени могут появиться сильные выбросы
помехи в противофазе с сигналом и тогда фаза результирующего вектора
станет неопределенной [вектор начнет вращаться вокруг начала координат,
например, по траектории а (см. рис. 6.2, а), возвращаясь после
окончания выброса в область вблизи точки А]. В этом случае произойдет скачок
фазы на ±2πn рад (где п = 1,2,...) и любой
частотный или фазовый демодулятор зафиксирует мгновенное аномальное изменение
(скачок) частоты или фазы (рисунок 6.2, б), так
как ![]() , и соответственно аномальный выброс
напряжения на выходе демодулятора, который приведет к аномальным
погрешностям при передаче непрерывных сообщений или к ошибкам при приеме
элементарного символа в цифровых системах передачи.
, и соответственно аномальный выброс
напряжения на выходе демодулятора, который приведет к аномальным
погрешностям при передаче непрерывных сообщений или к ошибкам при приеме
элементарного символа в цифровых системах передачи.
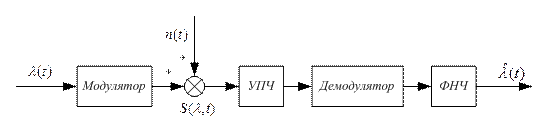
Рисунок 6.3
Из приведенного рассмотрения видно, что при любом методе приема УМ сигналов, помимо небольших (нормальных) флуктуации фазы и частоты, могут возникать аномальные выбросы, которые, как будет показано несколько позднее, и определяют пороговые свойства любого приемника УМ сигналов. Поэтому при анализе помехоустойчивости и пороговых свойств систем с угловой модуляцией необходимо учитывать нормальные и аномальные составляющие погрешностей.
Имеющиеся исследования показывают, что механизм воздействия на гармонический сигнал импульсных и синусоидальных помех хотя и несколько отличается от рассмотренного, однако также приводит к возникновению нормальных и аномальных погрешностей [12].
Помехоустойчивость
и пороговые свойства системы передачи с ЧМ и стандартным частотным
дискриминатором. Под стандартными понимаются различные частотные
дискриминаторы (на расстроенных и связанных контурах, дробные и т.п.).
Структурная схема расчетной модели рассматриваемой системы передачи приведена
на рисунке 6.3. В дальнейшем будет предполагаться, что передаваемое сообщение λ(t)
представляет собой случайный стационарный процесс с ограниченной спектральной
плотностью мощности, т. е. ![]() при
при ![]() и 0 ≤ ω ≤ 2πFc; полосовой
фильтр (усилитель промежуточной частоты УПЧ) является идеальным с полосой
пропускания, равной ширине спектра УМ сигнала, т. е.
и 0 ≤ ω ≤ 2πFc; полосовой
фильтр (усилитель промежуточной частоты УПЧ) является идеальным с полосой
пропускания, равной ширине спектра УМ сигнала, т. е. ![]() .
Фильтр низкой частоты ФНЧ идеальный с частотой среза Fcp = Fc.
На входе приемника действует помеха n(f) типа белого
гауссовского шума со спектральной плотностью мощности N0.
.
Фильтр низкой частоты ФНЧ идеальный с частотой среза Fcp = Fc.
На входе приемника действует помеха n(f) типа белого
гауссовского шума со спектральной плотностью мощности N0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.