Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи. Помехоустойчивость и пороговые свойства цифровых систем передачи непрерывных сообщений, страница 6

Помехоустойчивость квазиоптимального СФД. При частном синтезе СФД по минимуму дисперсии погрешности исходным уравнением является уравнение (6.11). После взятия интегра­лов в (6.11) получается выражение для дисперсии фазовой погрешности

,

где    —относительные параметры демодулятора (например, коэффициент усиления, постоянные времени и т. п.), от которых дисперсия по­грешности  зависит экстремально;

 — другие параметры сигнала или демодулятора.

Задача отыскания минимума дисперсии погрешности = min сводится в этом случае к нахождению минимума функции по несколь­ким переменным (где i = 1,2,...). Решением этой системы уравнений и будут являться выражения для оптимальных параметров и минимальной дисперсии демодуляции.

Следует отметить, что рассмотренные здесь методики полного и час­тичного синтезов оптимальных и квазиоптимальных СФД по минимуму дисперсии суммарной погрешности совпадают с задачей оптимизации таких демодуляторов по пороговому значению отношения сигнал-по­меха на входе.

В частности, при сообщении (t), определяемом выражением (2.116), и установке в петле СФД пропорционально интегрирующего фильтра

выражения для оптимальных параметров СФД и порогового значения отношения сигнал-шум при ЧМ приведены ниже [6,12]:

;

;

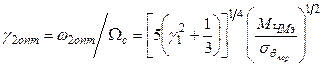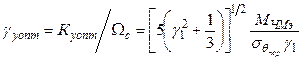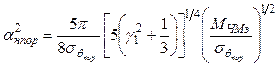
где - коэффициент усиления петли СФД; .

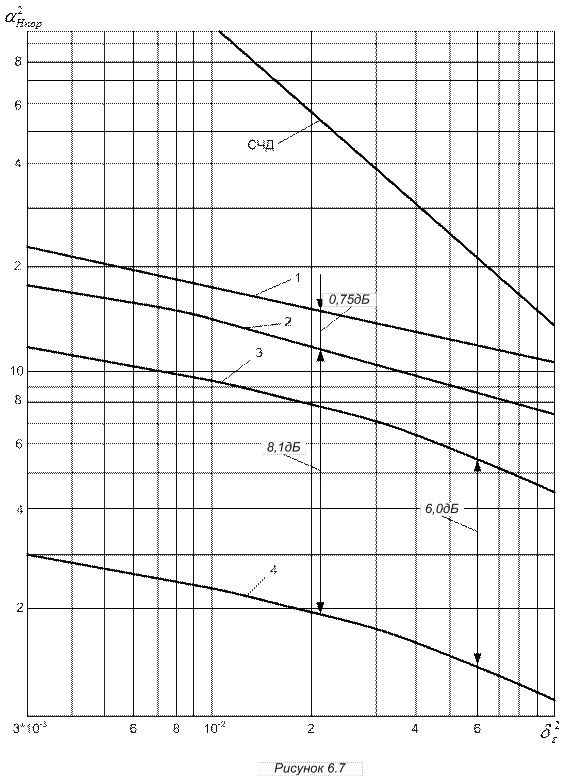
Сравнение различных методов приема ЧМ сигналов. Получен­ные в этом параграфе расчетные зависимости позволяют провести сравнение по помехоустойчивости различных методов приема ЧМ сигналов при работе в условиях флуктуационных помех типа бело­го гауссовского шума. Для нагляд­ности и удобства сравнения раз­личных методов приема ЧМ сигна­лов на рисунке 6.7 приведены прибли­женные зависимости, полученные для случая передачи непрерывного сообщения с равно­мерным спектром и условия, что широкополосность системы переда­чи выбирается оптимальной [13]. Кривая / приведена для оптималь­ного СФД второго порядка при = 0,25, кривая 2—для опти­мального физически реализуемого СФД при — 0,25, кривая 3 — для оптимальной физически нереализуемой системы с ФМ и СФД. Здесь же приведены зависимости для идеальной по Шеннону системы передачи (кривая 4) в предположении, что система занимает беско­нечно широкую полосу частот  [6, 12] и при приеме на СЧД.

На основании приведенных данных можно сделать следующие вы­воды:

1.  Система передачи с ЧМ и оптимальным физически реализуемым СФД требует примерно на 8 дБ большего порогового значения отноше­ния сигнал-помеха на входе, чем идеальная по Шеннону система пере­дачи.

2.  СФД второго порядка с оптимизированными параметрами про­ игрывает оптимальному физически реализуемому СФД по пороговому значению примерно 0,7—0,8 дБ.

3.  При высоких требованиях к качеству передачи сообщения (< 0,1) СФД по помехоустойчивости и пороговым свойствам значитель­но превосходят стандартный частотный дискриминатор. При сравни­тельно низких требованиях к качеству передачи (>0,1) хорошими пороговыми свойствами обладает  и СЧД.

4.  Помехоустойчивость и пороговые свойства рассмотренных поме­хоустойчивых демодуляторов (например, СФД) полностью реализуют­ся лишь при выборе оптимальной широкополосности которая должна быть несколько шире, чем при использовании менее помехоус­тойчивых демодуляторов (например, СЧД).

5. На помехоустойчивость систем передачи с ЧМ влияют не только вид демодулятора и его характеристики, а также и ограниченность ди­намического диапазона телефонного сигнала, использование предыска-жающих и корректирующих фильтров, а также компандирование речи. Применение, например, предыскажений спектра речевого сигнала с по­следующей обратной коррекцией на выходе приемника позволяет полу­чить выигрыш в снижении выходного шума на несколько децибел.