Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи. Помехоустойчивость и пороговые свойства цифровых систем передачи непрерывных сообщений, страница 3

4.  Спектральные плотности мощности помех на выходе амплитудного, фазового и частотного демодуляторов существенно раз­личны. При AM и ФМ S_n () равномерна, а при ЧМ имеет параболиче­ский характер.

5.  Хотя ЧМ и ФМ сигналы имеют между собой много общего, их помехоустойчивости заметно отличаются, причем при сообщении с ог­раниченным спектром более высокой помехоустойчивостью обладают ЧМ сигналы (см. табл. 6.1), а при сообщении с бесконечным спектром [например, вида формулы (2.11а)] более высокая помехоустойчивость у системы с ФМ сигналами.

6.  Можно показать, что вследствие лучшего использования мощности передатчика при БМ и ОМ и гармоническом модулирующем сообщении имеет место выигрыш в отношении сигнал-помеха на выхо­де по сравнению с AM в 3 раза. Этот выигрыш возрастает с увеличением пикфактора сообщения.

Оценка аномальных погрешностей. Как от­мечалось, необходимым условием появления аномальной погрешности на выходе приемника УМ сигналов является возникновение перескока фазы на 2рад во входном сигнале (на выходе усилителя проме­жуточной частоты). Поэтому задача оценки аномальных погрешностей на выходе приемника сводится прежде всего к оценке статистических характеристик  перескоков  фазы.

Оценка среднего числа перескоков фазы. Основные исследования ста­тистических характеристик перескоков фазы на входе СЧД выполне­ны в предположении, что имеет место достаточно большое значение от­ношения сигнал-помеха на входе, перескоки происходят достаточно редко и представляют собой простейший пуассоновский поток.

При приеме немодулированного несущего колебания, частота кото­рого расположена симметрично энергетическому спектру шума, сред­нее число перескоков в отрицательную и положительную стороны оди­наково и определяется как среднее число пересечений фазой уровня ±

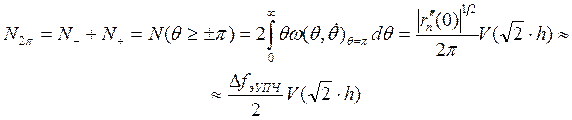
где  — двухмерная плотность, распределения фазы и ее производной , взятой при   =;

 — вторая   производная нормированной   корреляционной   функции шума  (помехи) в точке ее максимального значения (при = 0);

V (x) — интеграл  вероятности [см. формулу (2.13а)];

h² — отношение сигнал-шум на выходе усилителя промежуточной час­тоты.

В этой формуле

;

.

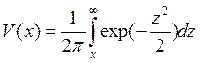Величина (0) однозначно связана с эффективной полосой пропус­кания усилителя промежуточной частоты и определяется формой его амплитудно-частотной характеристики.

При модуляции сигнала по частоте центрированным нормальным случайным процессом имеем

.                           (6.5)

Вероятность появления перескоков фазы на 2ли рад на выходе УПЧ и соответствующая ей вероятность возникновения аномальных погреш­ностей на выходе СЧД в интервале Т = l/(2F_c) будут определяться следующей приближенной зависимостью:

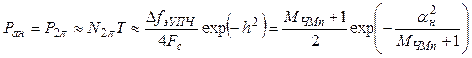.   (6.6)

В этой формуле принималось, что 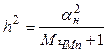 и .

Оценки дисперсии аномальных погрешностей. Если принять, что перескоки фазы и соответственно аномальные выбросы напряжения на выходе СЧД могут быть аппроксимированы в виде дельта-импульсов с площадью 2 и энергетическим спектром (2)², то N₂независимых перескоков создадут в области низких частот равномерную односто­роннюю спектральную плотность мощности:

,                                  (6.7)

где  Кчд— крутизна  характеристики СЧД.

Следовательно, мощность аномального шума на выходе фильтра низкой частоты в полосе О — F_c

.

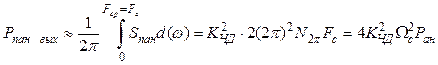С учетом выражений (6.5) и (6.6) имеем

.

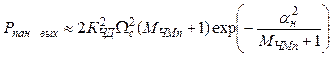Учитывая, что мощность сигнала на выходе СЧД определяется вы­ражением (6.4), отношение мощности сигнала к мощности аномального шума на его выходе (или значение приведенной к мощности сообщения дисперсии аномальной погрешности).

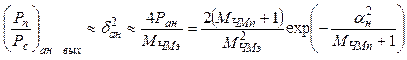          .       (6.8)

Заметим, что как и, так и „ зависит лишь от двух параметров: и . Однако если с увеличением уменьшаются и  и  (что вполне естественно), то с возрастанием  уменьшается , a увеличивается.

Оценка суммарной погрешности, явление порога и оптимизация параметров. Полученные зависимости для  и Р_ан полностью характеризуют систему передачи с УМ и СЧД. Однако на практике качество передачи часто характери­зуется суммарной средней квадратичной погрешностью  или отно­шением мощности сигнала к суммарной мощности шума на выходе СЧД .