Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи. Помехоустойчивость и пороговые свойства цифровых систем передачи непрерывных сообщений, страница 8

Оценка погрешности квантования при ДИКМ. При разностном представлении квантуются выборки, затем образуются конечные разности (см. §2.6). Поскольку они получены из выборок, шаг кванто­вания их значений  можно принять таким же, как и для выборок, однако диапазон значений конечных разностей (шкала) будет мень­ше. При гауссовском законе распределения процесса  такой же закон распределения будет и у конечных разностей, поэтому их шкалу мож­но принять равной, [где  — среднее квадратичное откло­нение конечной разности] (см. таблицу 2.7). В остальном методика оценки погрешности квантования аналогична соответствующей методи­ке для дискретизаций выборками. Учитывая сказанное и заменяя  на , вместо формулы (6.22) получим

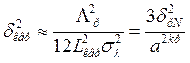                               (6.23)

где — приведенная дисперсия конечной разности (t) порядка N (см. таблицу 2.7);

 k_р — число   разрядов   кода, используемого для представления конечных разностей.

Заметим, что при ДИКМ обычно берется а = 2.

В формуле (6.23)

Из сопоставления выражений (6.22) и (6.23) для приведенных дис­персий погрешности квантования при ИКМ и ДИКМ видно, что при одинаковом числе уровней квантования (L_кв или а и k) дисперсия по­грешности квантования при ДИКМ в раз меньше, чем при ИКМ.

Оценка аномальных погрешностей при ИКМ. Под действием флук-туационных помех в канале передаваемые дискретные сигналы искажа­ются, в результате чего вместо одного значения кодового слова (выборки сообщения) фиксируется другое, т. е. возникают аномальные по­грешности. Аномальные погрешности в цифровых системах передачи с ИКМ могут принимать лишь дискретные значения _ан = (где  — значение аномальной погрешности, выраженной числом шагов квантования и принимающей значения (L_KB — 1) ≤  ≤ (L_KB + 1)). Указанные погрешности характеризуют достоверность передачи сооб­щений. В качестве критерия достоверности целесообразно использо­вать или вероятность появления аномальной погрешности при переда­че одного отсчета (координаты) сообщения р_ан. или приведенную дис­персию аномальной погрешности ²_ан.

Оценка вероятности аномальных погрешностей р_ан при ИКМ. В общем случае в кодовой комбинации, со­стоящей из k символов, может быть искажено от одного до всех k сим­волов. Вполне очевидно, что вероятность аномальной погрешности р_ан (вероятность того, что кодовая комбинация будет принята хотя бы с одной ошибкой) зависит и от вероятности искажения элементарного символа р_ош и закономерности распределения ошибок, характерной для того или иного канала передачи.

В гауссовских каналах передачи ошибки при приеме элементарных символов в кодовой группе с простым кодированием можно считать не­зависимыми, т. е. вероятность искажения каждого из разрядов кодо­вой комбинации одинакова и постоянна. Для этого случая вероятность того, что среди кодовой комбинации длиной в k символов встретится ровно  l ошибочных, может быть определена на основании формулы Бер­ну лли

В этой формуле C^l_k — число сочетаний из k по l (l — кратность ожи­даемой ошибки):

C^l_k=k!/[l!(k—l\!].                                       (6.24)

Напомним (см. § 5.6), что вероятность ошибки в одном разряде слова р_ош зависит от метода передачи (основания кода, метода манипуляции и коэффициента взаимной корреляции между сигналами), метода при­ема, вида помехи и отношения сигнал-помеха на входе приемника.

В общем случае вероятность появления аномальной ошибки в прие­ме кодового слова (вероятность того, что кодовая комбинация будет принята хотя бы с одной ошибкой)

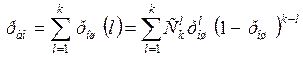.               (6.25)

При kp_oш << 1 вероятность р_ош (l) быстро уменьшается с ростом l и подавляющую долю ошибок составляют одиночные ошибки. В этом случае сумма (6.25) хорошо аппроксимируется первым членом:

         (6.26)

Из полученного выражения видно, что р_ан зависит от качества ка­нала  передачи, характеризуемого   р_ош, и длины кодового слова k.

Оценка дисперсии аномальной погрешно­сти. При использовании простых кодов дисперсия аномальной по­грешности может быть найдена на основании общего правила опреде­ления дисперсии случайных величин.