Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи. Помехоустойчивость и пороговые свойства цифровых систем передачи непрерывных сообщений, страница 2

Оценка нормальных погрешностей. Нор­мальные погрешности будем оценивать по отношению сигнал-помеха на выходе приемника (Р_с/Рп)_вых  1/°1- Поскольку мы рассматрива­ем работу системы при большом значении отношения сигнал-помеха, т. е. в линейном режиме без учета аномалий, то на основании исполь­зования принципа суперпозиции мощности сигнала и шума на выходе приемника могут рассчитываться раздельно. При этом динамические погрешности учитываться не будут.

Условие большого значения отношения сигнал-помеха обычно за­писывают так

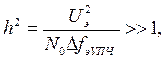
где — отношение мощности сигнала  к мощности шума в полосе пропуска­ния  приемника  

Дополнительно будем также предполагать, что стандартный частот­ный дискриминатор (СЧД) по отношению к частоте сигнала является простым усилительным звеном, а по отношению к фазе сигнала (так как — идеальным дифференцирующим звеном с комплекс­ным коэффициентом передачи  [где— коэф­фициент передачи (крутизна характеристики) СЧД].

В соответствии с принятым допущением и выражением (6.3) напря­жение полезного сигнала на выходе частотного демодулятора (с учетом того, что номинальная частота демодулятора совпадает со значением несущей )

.

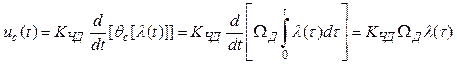Не теряя общности, полное сопротивление нагрузки на выходе СЧД предполагается равным единице.

Соответственно спектральная плотность мощности и мощность по­лезного сигнала на выходе СЧД будут определяться выражениями:

 при ;                    (6.4)

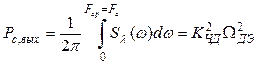
При этом не учитывается эффект подавления сигнала при переско­ках фазы.

С учетом подавления сигнала

,

где  — вероятность появления перескока фазы за время .

Напряжение нормальной помехи на выходе СЧД в свою очередь с учетом выражения (6.3)

.

Спектральная плотность мощности помехи

,

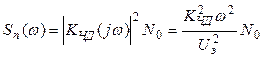т. е. имеет форму параболы. Отметим, что такая неравномерность спект­ральной плотности мощности помехи на выходе СЧД будет приводить к более сильному искажению высокочастотных составляющих спектра сообщения. Для борьбы с этим явлением в системах с ЧМ часто на пере­дающей стороне вводят предыскажения сообщения (подъем уровня вы­сокочастотных составляющих).

Мощность нормального шума (помехи) на выходе демодулятора

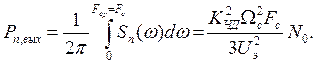
Соответственно отношение мощности сигнала к мощности помехи (шума) на выходе приемника или приведенная дисперсия нормальной погрешности

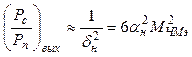
где  —отношение мощности сигнала   к мощности  шума в  удвоенной   инфор­мативной полосе сообщения;

— эффективный  индекс частотной модуляции.

В этой формуле

,  .

Заметим сразу же, что значение приведенной дисперсии нормальной погрешности зависит лишь от двух параметров: индекса частотной мо­дуляции  и отношения сигнал-помеха в удвоенной полосе сообще­ния .

Аналогично полученные выражения для  при ис­пользовании других видов модуляции для сообщения с ограниченным спектром приведены в табл. 6.1.

На основании полученных выражений можно сделать ряд важных выводов.

1. Для всех рассмотренных непрерывных систем модуляции отно­шение сигнал-помеха (шум) на выходе приемника при большом значе­нии отношения сигнал-помеха на входе прямо пропорционально квад­рату эффективного   индекса соответствующей модуляции М² и отно­шению сигнал-помеха на входе .

Однако следует иметь в виду, что увеличивать беспредельно широкополосность системы передачи с угловой модуляцией (индекс моду­ляции) ^ПР^И фиксировании значений нельзя, так как при этом не будет соблюдаться условие большого значения отношения сиг­нал-помеха на входе демодулятора и полученные формулы будут не­верны вследствие частого появле­ния аномальных погрешностей (пе­рескоков фазы).

2.    В системах с угловой модуляцией можно получить выигрыш в  ­
помехоустойчивости по сравнению с AM расширением спектра сигнала-
переносчика.

Выигрыш  (при М_АМ = 1   и ):

;   .

3.  При выводе соотношений для (Р_с/Р_п)_выхфактически не накладывалось никаких принципиальных ограничений (например, на полосу пропускания приемника до демодулятора). Это означает, что полученные соотношения действительны для любых типов приемников (оптимальных, квазиоптимальных, реальных), т. е. эти же результаты получаются и на основании теории оптимального приема.