Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи. Помехоустойчивость и пороговые свойства цифровых систем передачи непрерывных сообщений, страница 5

Помехоустойчивость таких демодуляторов оценивается на основа­нии статистической теории систем автоматического регулирования (теории линейной фильтрации). Если предположить, что полезный, на­пример ФМ сигнал и белый шум статистически независимы и заданы своими спектральными плотностями, то в установившемся линейном режиме дисперсия фазовой погрешности слежения, характеризующая точность слежения и демодуляции, будет определяться выражением вида (5.84):

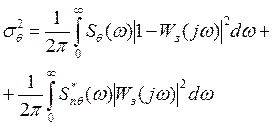                                                         (6.11)

где — спектральная плотность мощности фазы полезного сигнала;

— эквивалентная спектральная плотность фазового шума, приведен­ная ко входу фазового дискриминатора;

— передаточная функция замкнутого демодулятора относительно фазы сигнала.

В формуле (6.11)

;

где— передаточная функция модулятора (при использовании, напри­мер, фазового модулятора   );

                                      ;

                                      .

В последнем выражении — передаточная функция разомк­нутой системы, равная произведению передаточных функций отдель­ных звеньев, определяемая соотношением

,

где  — коэффициент передачи линеаризированного фазового   детектора;

 —  лередаточная функция ФНЧ1 в петле;

 — передаточная функция ЧМГ.

Случайное сообщение (t) на выходе системы воспроизводится в ви­де оценки (t). Качество передачи сообщения обычно характеризует­ся или приведенной средней квадратичной (дисперсией) погрешностью, или отношением мощности сигнала к мощности шума на выходе .

Оценка качества передачи сообщения и соответственно помехоустой­чивости системы передачи в целом и следящего демодулятора в частно­сти по величине  или является недостаточной. Необходимо еще как-то охарактеризовать появление аномальных погрешностей, присущих широкополосным системам при любых методах приема и ха­рактеризующих надежность работы СФД.

Надежность работы СФД косвенно может оцениваться по так назы­ваемой пороговой дисперсии фазовой ошибки . Исходя из экспериментальных данных обычно

.                                    (6.12)

Считается, что при указанном значении обеспечивается близ­кий к линейному режим работы СФД и допустимая вероятность появ­ления перескоков фазы (аномальных погрешностей).

Синтез и помехоустойчивость оптималь­ного линеаризированного СФД. В общем случае при рассмотрении системы передачи могут решаться задачи анализа и пол­ного или частичного (оптимизации параметров) синтеза такой системы или демодулятора.

В частности, при выборе оптимальной физически реализуемой пере­даточной функции линеаризованного СФД минимизации выражения (6.11) при фазовой модуляции и спектральной плотности мощности со­общений, определяемой полиномом Баттерворта (2.11) на осно­вании использования выражения (5.88), приводит к следующему вы­ражению для минимальной дисперсии фазовой погрешности слежения:

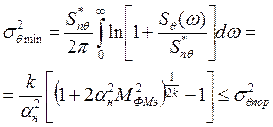                             .                     (6.13)

В этой формуле — отношение мощности сигнала к мощности шу­ма в удвоенной эффективной полосе сообщения:

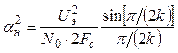
где k —степень  полинома   Баттерворта [см. формулу (2.11)].

Соответственно приведенная дисперсия погрешности

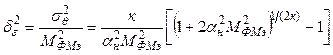.               (6.14)

Из формулы (6.14) видно, что  уменьшается с увеличением и . Однако, как в любой широкополосной системе, обратно пропор­циональная зависимость  от будет соблюдаться лишь в надпороговой области, т. е. в области больших значений. При приеме УМ сигналов на СФД надпороговый режим работы СФД будет иметь место до тех пор, пока дисперсия фазовой ошибки, определяемая выраже­нием (6.12), будет меньше порогового значения

Полученные таким образом выражения для оценки помехоустойчи­вости систем передачи определяют потенциальные возможности систе­мы передачи с ФМ и СФД [13]. Однако при k > 1 оптимальные переда­точные функции СФД трудно реализуемы и поэтому выражения для по­рогового показывают предел, к которому лишь можно стремиться. В связи с этим часто используются квазиоптимальные СФД с заданной передаточной функцией и оптимальными параметрами. Рассмотрим ко­ротко методику нахождения оптимальных параметров у линеаризован­ного квазиоптимального СФД [13].