Помехоустойчивость и пороговые свойства аналоговых непрерывных систем передачи. Помехоустойчивость и пороговые свойства цифровых систем передачи непрерывных сообщений, страница 10

Оценка суммарной погрешности. Явление порога и оптимизация параметров ЦСП с ИКМ. Учитывая, что погрешности интерполяции, квантования по уровню и аномальные (от помех в канале) в системах с ИКМ, можно считать приближенно независимыми, выражение для при­веденной дисперсии суммарной (результирующей) погрешности в рас­сматриваемых цифровых системах передачи можно представить в виде

где  — приведенная дисперсия интерполяционной погрешности;

     — коэффициент фильтрации   интерполирующего   устройства по отноше­нию к   шумам квантования и канала (см. § 2.5).

При передаче случайных величин или когда интерполяционную по­грешность можно не учитывать,

                       (6.35)

Рассмотрим этот случай несколько подробнее. При передаче слу­чайных величин с гауссовским законом распределения с помощью ИКМ на основании выражений (6.22) и (6.32) приведенная дисперсия суммарной погрешности

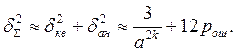
В частности, при оптимальном некогерентном приеме многоос­новных ортогональных сигналов (например, вида ИКМ_а-ЧМ) разверну­тое выражение для приведенной дисперсии суммарной   погрешности

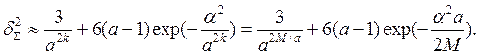   (6.36)

В формуле (6.36) вероятность ошибки в опознании элементарного символа р_ош при заданных сигналах и методе приема определялась с учетом выражения (5.70) по формуле

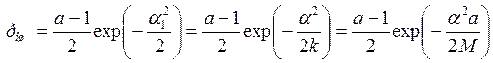
где  — отношение энергии сигнала (Е ~ E_xk), отводимой для передачи кодо­вого слова (одного отсчета сообщения) к спектральной плотности мощ­ности шума N₀;

       М  — число степеней свободы сигнала-переносчика, приходящихся на одно кодовое слово (один отсчет сообщения).

В этой формуле

где -ширина   спектра сигнала-переносчика;

      время, отводимое для передачи кодового слова.

Ширина спектра сигнала-переносчика

Время, отводимое для передачи кодового слова, . В част­ности, при ИКМ-ЧМ сигналах определяется выражением (3.20). Обратим внимание на то, что в цифровых системах передачи число М иг­рает ту же роль, что и индекс соответствующей модуляции в аналого­вых широкополосных системах.

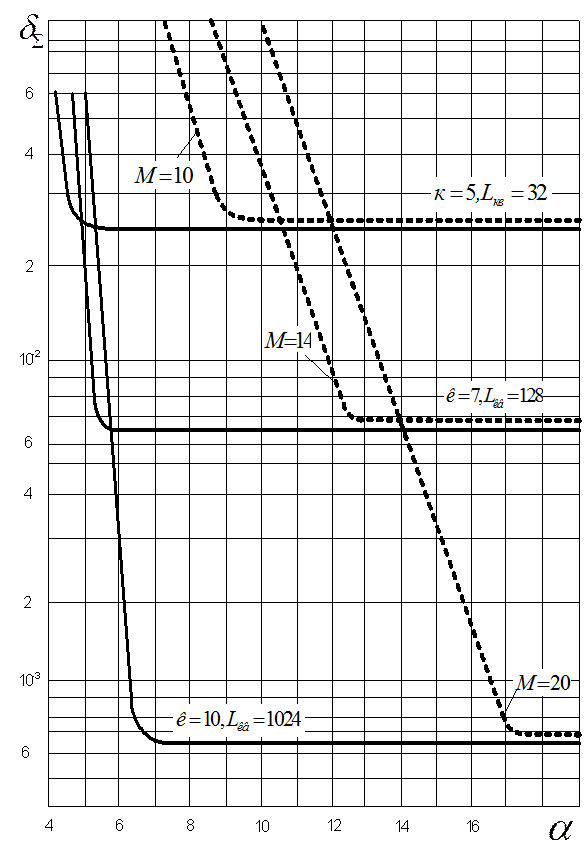
Результаты расчета зависимости по формуле (6.36) для значений k= 5,7, 10 и L_KB = 2⁵, 2⁷, 2¹⁰, для двоичных сигналов вида ИКМ₂-ЧМ и ортогональных вида КАИМ-ЧМ сигналов (когда каждый уровень передается своим ортогональным ко всем остальным сигналом, т. е. а = L_KB) приведены на рис. 6.12. Как видно, зависимо­сти, как и в аналоговых широко­полосных системах передачи, но­сят ярко выраженный пороговый характер.

Пороговый характер такой зависимости проявляется в том, что
при определенных значениях а² небольшое его уменьшение приводит к достаточно резкому увеличе­нию суммарной погрешности. Как и в аналоговых широкополосных системах передачи с УМ и ФИМ, причиной этого эффекта являются аномальные погрешности, вклад которых в резко возрастает по мере уменьшения а² ниже некоторого значения, часто  называемого пороговым. Как и в аналоговых широкополосных системах передачи (см. § 6.2 и 6.3), рассматриваемые зависимости могут быть разбиты на три области: надпороговую, пороговую и подпороговую. Отличие приведенных зависимостей от подобных зависимостей для широкополосных аналоговых непрерывных и импульсных систем пе­редачи состоит в том, что в цифровых системах передачи при значе­ниях , больших пороговых,  остается постоянной (определяется погрешностью квантования), в то время как в аналоговых системах передачи погрешность

                                                            Рисунок 6.12

 уменьшается (Определяется нормальной погрешностью) с увеличением .

Из полученных выражений и графиков видно, что при использова­нии для передачи непрерывных сообщений дискретных сигналов (как и широкополосных сигналов) существует оптимальное число (оп­тимальная широкополосность), при котором заданное значение обеспечивается при минимальном пороговом значении отношения сиг­нал-шум ²_пор.

Из приведенных зависимостей также видно, что система передачи, использующая М ортогональных (КАИМ-ЧМ) сигналов, обладает бо­лее высокой помехоустойчивостью, чем система, использующая двоич­ные (ИКМ-ЧМ) сигналы [излом характеристики наступает при меньших значениях ], что согласуется с данными § 5.6.