7
Процедурыоценивания
ЦелиизученияК концу этой главы вы сможете:
1. Объяснить логику оценивания и роль выборки, распределения выборочных статистик и генеральной совокупности.
2. Определить и объяснить понятия смещения и мощности.
3. Строить и объяснять доверительные интервалы для выборочных средних и выборочных долей.
4. Объяснить связь между доверительным уровнем, размером выборки и шириной доверительного интервала.
7.1. Введение
Целью этого вида
статистических выводов является оценивание значений или параметров генеральной
совокупности на основании вычисленных выборочных ста-гистик. Хотя методы,
представленные в этой главе, может быть и новы для вас, вы определенно знакомы
с наиболее распространенными сферами их применения: опросы общественного
мнения и прогнозы результатов выборов. Опросы и обследо-;ания по всем
мыслимым вопросам, от очень важных до самых незначительных, стали одним из
главных продуктов средств массовой информации и современной культуры. Методы,
которые вы изучите в данной главе, практически идентичны тем, которыми
пользуются самые респектабельные и широко использующие научные до-ртижения компании,
занимающиеся проведением опросов.
Существует два вида процедур оценивания. Первый вид, точечная оценка, представляет собой выборочную статистику, используемую для оценивания соответствующего параметра генеральной совокупности. Например, когда статья в газете :ообщает, что, основываясь на результатах опроса общественного мнения, 74% аме-жканцев поддерживают смертную казнь, она приводит точечную оценку. Второй вид троцедур оценивания включает доверительные интервалы, которые содержат диапа-юн значений (интервал), а не одну точку. Вместо того чтобы давать оценку в виде конкретного числа, как в случае точечной оценки, интервальная оценка может быть сформулирована в следующем виде: "от 39% до 45% электората проголосует за данного кандидата". В последней оценке мы предполагаем, что это значение для генеральной совокупности находится между 39% и 45%, но не указываем, где именно.
Глава 7. Процедуры оценивания 197
7.2. Смещениеиэффективность
И при точечном, и при
интервальном оценивании в качестве статистических оценок используются выборочные статистики.
Какую из множества доступных выборочных
статистик следует использовать? Статистические оценки могут быть выбраны на основании двух критериев: смещения и
эффективности. Статистическая оценка
является несмещенной тогда и только тогда, когда среднее значение распределения
ее выборочных статистик равно интересующему значению генеральной совокупности. Из теорем, представленных в главе 6,
мы знаем, что средние значения выборок
соответствуют этому критерию. Среднее значение распределения выборочных средних (которое мы символически обозначим Цц)
равно среднему значению генеральной совокупности (/л).
Выборочные пропорции (Р) являются также несмещенными. Поэтому, если мы вычислим выборочные пропорции для повторно извлекаемых случайных выборок размера N, а потом представим их на графике, то распределение выборочных пропорций будет иметь среднее значение (jij, равное пропорции для генеральной совокупности (Р). Таким образом, если нас интересуют испытания с подбрасыванием монет, и каждая выборка содержит 10 монет (N= 10), среднее значение выборочного распределения составит 0,5, что равно вероятности того, что при подбрасывании монета упадет орлом (или решкой) кверху. Все статистические показатели, за исключением выборочного среднего и выборочной пропорции, являются смещенными (то есть среднее распределения выборочных средних не равно среднему генеральной совокупности)1.
Нам известно, что выборочные средние и пропорции являются несмещенными, поэтому мы можем определить вероятность того, что они содержатся в некотором интервале значений генеральной совокупности, который мы пытаемся оценить. Для примера рассмотрим конкретную задачу. Предположим, что мы хотим оценить средний доход в генеральной совокупности. Была взята случайная выборка (N= 500), и было определено, что выборочное среднее равно $35000. Заметьте, что мы не имеем ни малейшего понятия, чему равно значение генеральной совокупности /л (если бы мы это знали, нам бы не нужна была выборка), но именно \iнас и интересует. Выборочное среднее, равное $35000, представляет для нас важность и интересует нас постольку, поскольку оно может дать нам информацию о генеральной совокупности.
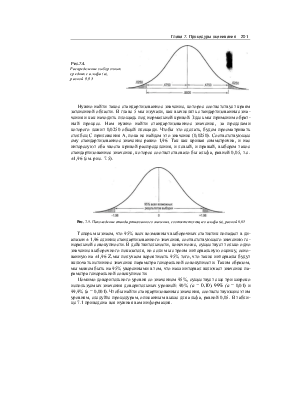
Две теоремы, приведенные в главе 6, дают нам много информации о распределении средних значений выборок. Так как ./V велико, мы знаем, что распределение выборочных средних является нормальным, и что его среднее значение равно среднему значению для генеральной совокупности. Мы также знаем, что все нормальные кривые содержат примерно 68% наблюдений (наблюдениями здесь являются средние значения выборок) в пределах ±1 Z, 95% наблюдений в пределах ±2 Z, и более чем 99% наблюдений в пределах ±3 Z. Помните, что мы обсуждаем распреде-
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.