Экономика и менеджмент \ Статистика

Процедуры оценивания. Смещение и эффективность. Процедуры интервального оценивания выборочных средних, страница 5

7.4. Процедурыинтервальногооцениваниявыборочных средних

Формула построения доверительного интервала, основанного на выборочных средних, имеет следующий вид:

Формула 7.1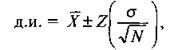

где:    д.и. — доверительный интервал;

  — выборочное среднее;

N — стандартизованное значение, определяемое уровнем альфа;

 –стандартное отклонение распределения выборочных средних или стандартная ошибка среднего.


Глава 7. Процедуры оценивания     203

Для примера, предположим, что вы хотите определить среднее значение коэф­фициента развития интеллекта (IQ) в некоторой группе людей, из которой вы слу­чайным образом сформировали выборку из 200 человек, для которой среднее зна­чение IQ составило 105. Допустим, что стандартное отклонение значений IQ приблизительно равно 15, так что установим о = 15. Если нас устраивает 5%-ая ве­роятность ошибиться и зададим альфа, равной 0,05, тогда соответствующее стандар­тизованное значение будет равно 1,96. Подставив эти значения напрямую в форму­лу 7.1, мы получим интервал:

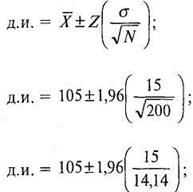
д.и. = 105 ±(1,96)(1,06); д.и. = 105 ±2,08 .

Таким образом, наша оценка показывает, что истинное среднее значение коэф­фициента IQ для рассматриваемой генеральной совокупности находится где-то меж­ду 102,92 (105 - 2,08) и 107,08 (105 + 2,08). Так как 95% всех возможных выбороч­ных средних находится в пределах ±1,96 Z(в данном случае, 2,08 единиц IQ) от среднего значения распределения выборочных средних, велики шансы того, что наш интервал будет включать среднее значение генеральной совокупности. В действи­тельности, даже если выборочное среднее будет находиться на расстоянии ±1,96 Z(что маловероятно), наш интервал все еще будет содержать , а значит и μ. Нам не удастся включить среднее значение генеральной совокупности только в том слу­чае, если наше выборочное среднее будет одним из тех немногих значений, которые находятся за пределами ±1,96 Z от среднего значения распределения выборочных средних.

Обратите внимание на то, что в примере, приведенном выше, у нас было значе­ние стандартного отклонения генеральной совокупности. Не приходится и говорить, что то, что мы обладаем такой информацией о генеральной совокупности, доволь­но необычно. В абсолютном большинстве случаев мы не будем знать значения а. Однако в таких случаях мы можем заменить значение сего оценкой, s(выборочным стандартным отклонением). К сожалению, sявляется смещенной оценкой, и для того чтобы ее скорректировать, формулу следует немного изменить. Для выборок боль­шего размера смещение sне будет значительно влиять на интервал. Скорректиро­ванная формула для случаев с неизвестным значением а имеет следующий вид:


204    Часть II. Статистические выводы


 

Формула 7.2


При сравнении этой формулы с 7.1 обратите внимание на то, что было внесено два изменения. Во-первых, σ было заменено на s, а во-вторых, в знаменателе после­днего выражения стоит квадратный корень от N — 1, а не квадратный корень от N. Это изменение является корректировкой того факта, что sявляется смещенной оцен­кой.

Здесь необходимо сказать, что замена sна σ возможна только для больших выбо­рок (т.е. для выборок, состоящих из 100 и более наблюдений). Для выборок меньших размеров, в которых неизвестно значение стандартного отклонения генеральной совокупности, стандартное нормальное распределение, приведенное в приложе­нии А, не может быть использовано в процессе оценивания. Существует возмож­ность построения осмысленных интервальных оценок для выборок, содержащих меньше 100 наблюдений, но для этого нам следует использовать другое теоретичес­кое распределение, которое называется t-распределением Стьюдента, для нахожде­ния площади под распределением выборочных статистик. Мы отложим рассмотре­ние t-распределения до главы 8, а пока заострим свое внимание на процедурах оценивания, предназначенных только для больших выборок.

В завершении этого раздела давайте рассмотрим задачу-пример, в которой ис­пользуется формула 7.2. Средний доход в случайной выборке из некоторой группы людей составляет $35000, причем стандартное отклонение равно $200. Чему равна 95%-ная интервальная оценка среднего значения генеральной совокупности,  μ?

Исходя из того, что:

X= $35000; s= $200; N=500; и используя уровень альфа 0,05, можем построить интервал:

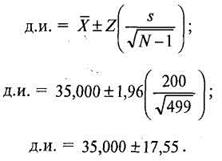
Значение среднего дохода для этой группы находится в пределах от $34982,45 (35000 - 17,55) и $35017,55 (35000 + 17,55). Помните, что вероятность того, что этот интервал ошибочен (т.е., что он не включает среднее значение генеральной совокуп­ности), составляет всего лишь 5%. В качестве практического задания, касающегося доверительных интервалов для выборочных средних, см. задачи 7.1, 7.4—7.7, 7.18 и 7.19a-7.19в

Скачать файл