Экономика и менеджмент \ Статистика

Процедуры оценивания. Смещение и эффективность. Процедуры интервального оценивания выборочных средних, страница 6


Глава 7. Процедуры оценивания    205

7.5. Процедурыинтервальногооцениваниядлявыборочных пропорций (большиевыборки)

Процедуры оценивания выборочных пропорций в значительной степени похо­жи на процедуры оценивания выборочных средних. Основное различие заключает­ся в том, что так как пропорции представляют собой статистический показатель, отличный от средних значений, мы должны использовать другое распределение вы­борочных статистик. В действительности, опять же исходя из центральной предель­ной теоремы, мы знаем, что пропорции выборки имеют нормальные распределения выборочных статистик со средними значениями (μр), равными значению генераль-ной совокупности (Ри), и стандартными отклонениями (σp), равными  . Формула построения доверительных интервалов на основании выборочных пропор­ций имеет следующий вид:

Формула 7.3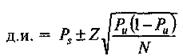

Значения Рsи N мы получаем напрямую из выборки, а значение Z определяется доверительным уровнем, как и в случае со средними значениями выборок. У нас в формуле остается одна неизвестная, Ри — то значение, которое мы и пытаемся най­ти. Эту дилемму можно решить, установив для Ри значение 0,5. Так как в числителе второе выражение, находящееся под знаком корня, (1—Рu), обратно Рu, все выраже­ние будет иметь значение 0,5 х 0,5, или 0,25, что представляет собой максимальное значение, которое только может принять это выражение. То есть, если мы устано­вим для Ри любое значение, отличное от 0,5, значение выражения Ри(1—Ри) будет уменьшаться. Например, если мы установим для Ри значение 0,4, второе выражение (1—Ри) будет равно 0,6, и значение всего выражения снизится до 0,24. Устанавливая; для Р значение 0,5, мы обеспечиваем, что выражение Рu(1—Рu) примет максималь­но возможное значение и, следовательно, интервал будет иметь наибольшую шири­ну. Такое решение, заключающееся в присвоении Ри в уравнении оценивания неко­торого значения, является наиболее осторожным из возможных решений.

Чтобы проиллюстрировать работу этих процедур, предположим, что вам нужно оценить пропорцию студентов вашего университета, пропустивших в прошедшем семестре, по меньшей мере, один день занятий по болезни. Из 200 студентов, вошедших в случайную выборку, 60 сообщили, что они были больны и пропустили занятия в прошедшем семестре, по меньшей мере, однажды. Таким образом, значение выборочной пропорции, которое мы будем использовать, равно 60/200, или 0,30. При доверительном уровне 95% интервальная оценка будет равна:


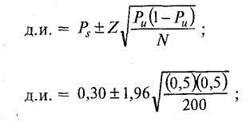
206    Часть II. Статистические выводы

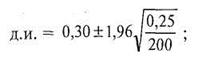
д.и. = 0,30 ± (1,96Х0,035);

Д.и. = 0,30+0,07.

На основании этого значения выборочной пропорции, равного 0,30, мы можем казать, что величина пропорции студентов, пропустивших, по меньшей мере, один день занятий по болезни, находится между 0,23 и 0,37. Оценку, конечно же, можно было выразить и в процентах, указав, что от 23% до 37% студентов болели в течение прошедшего семестра. В качестве практического задания, касающегося доверитель­ных интервалов для выборочных пропорций, см. задачи 7.2, 7.8—7.12 и 7.19г—7.19ж.

Практическийпример 7.1

Исследование среди американцев, касающееся времяпровождения после рабо­ты, было проведено с использованием выборки, состоящей из 1000 семей. В ка­честве главного вида такого времяпровождения респонденты указали просмотр телевизора. Чему равна оценка среднего значения генеральной совокупности, если выборка свидетельствует, что средняя продолжительность просмотра теле­визора составляет 6,2 часа в день? По выборке была получена следующая инфор­мация:

X   =6,2;

s = 0,7;

N = 1000.

д.и. = 6,2±(1,9бХ0,22); Д.и. = 6,2 ±0,04.

Если мы возьмем уровень альфа 0,05, соответствующее стандартизованное зна­чение будет равно ±1,96, и 95%-ный доверительный интервал будет иметь сле­дующий вид:


Глава 7. Процедуры оценивания     207

На основании этого результата мы можем вычислить, что все субъекты генераль­ной совокупности тратят на просмотр телевизора в среднем 6,2 ± 0,04 часов в день. Нижняя граница нашей интервальной оценки (6,2 — 0,04) равна 6,16, а вер­хняя граница (6,2 + 0,04) равна 6,24. Таким образом, этот интервал можно было указать другим способом:

6,16 £ μ £ 6,24.

Скачать файл