Подводя итоги, можно сказать, что так как стандартное отклонение распределения выборочных статистик является обратной функцией N, то чем больше выборка, тем больше степень группирования и тем выше эффективность. Отчасти можно сказать, что эта связь между размером выборки и стандартным отклонением распределения выборочных статистик всего лишь подтверждает интуитивно понятную идею о том, что большие выборки вызывают гораздо больше доверия, чем малые (при условии, что обе были сформированы случайным образом).
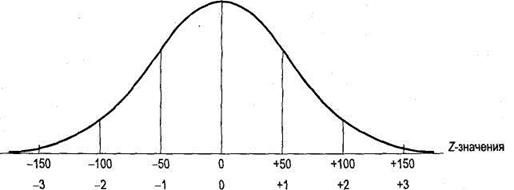
Рис. 7.2. Распределение
выборочных средних с N= 100 и 
= $50,00
2 В действительности, конечно же, значение а будет неизвестно.
200 Часть II. Статистические выводы
|
|
Рис. 7.3.
Распределение
выборочных средних с N= 1000 и = $15,81
7.3. Процедурыоценивания: введение
Процедура построения
точечной оценки довольно проста. В соответствии с правилом МРВО получаем
выборку, вычисляем либо пропорцию, либо среднее значение, и считаем, что
параметр генеральной совокупности равен выборочной статистике. Помните, что
чем больше выборка, тем выше эффективность, и тем больше вероятность того,
что статистическая оценка будет приблизительно равна значению для генеральной
совокупности. Также помните, что какой бы строгой не была процедура
формирования выборки, и какой бы большой не была выборка, всегда существует
большая вероятность того, что статистическая оценка является неточной.
В сравнении с точечными оценками интервальные оценки более сложны, но и более надежны, потому что когда мы приводим диапазон значений, высока вероятность того, что мы включим в него и параметр, отвечающий всей генеральной совокупности. Первый шаг при построении интервальной оценки заключается в том, чтобы выбрать риск ошибиться, который вы согласны принять. Интервальная оценка является неверной, если она не включает параметр, отвечающий всей генеральной совокупности. Вероятность ошибки называется альфа (обозначается а). Точное значение альфа зависит от природы исследования, но наиболее распространена вероятность, равная 0,05. Если альфа равна 0,05, что соответствует доверительному уровню 95%, это означает, что в перспективе исследователь согласен на то, чтобы можно ошибиться лишь в 5% случаев. Другими словами, если при данном уровне альфа (и при условии, что все остальные показатели сохраняют свои значения) построить бесконечное число интервалов, то 95% из них будут включать значение для генеральной совокупности, а 5% не будут. В действительности, конечно же, строится только один интервал, и, устанавливая низкое значение вероятности ошибки, мы склоняем шансы в свою пользу, т.е. в пользу того, что интервал будет включать значение для генеральной совокупности.
Вторым шагом является изображение распределения выборочных статистик, разделение вероятности ошибки на равные правый и левый хвосты кривой распределения и последующее нахождение соответствующего Z-значения. Например, если мы зададим альфа равной 0,05, тогда мы должны отнести половину (0,025) этой вероятности к левому хвосту, а половину — к правому хвосту распределения. Таким образом, распределение выборочных статистик будет разделено, как показано на рис. 7.4.
Глава 7. Процедуры оценивания 201
 |
|
Рис. 7.4.
Распределение выборочных средних с альфа (а), равной 0,05
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
