Нужно найти такое стандартизованное значение, которое соответствует краям затененной области. В главе 5 мы изучали, как вычислять стандартизованные значения и как находить площадь под нормальной кривой. Здесь мы применим обратный процесс. Нам нужно найти стандартизованное значение, за пределами которого лежит 0,0250 общей площади. Чтобы это сделать, будем просматривать столбец С приложения А, пока не найдем это значение (0,0250). Соответствующее ему стандартизованное значение равно 1,96. Так как кривая симметрична, и нас интересуют оба хвоста кривой распределения, и левый, и правый, выберем такое стандартизованное значение, которое соответствовало бы альфа, равной 0,05, т.е. ±1,96 (см. рис. 7.5).
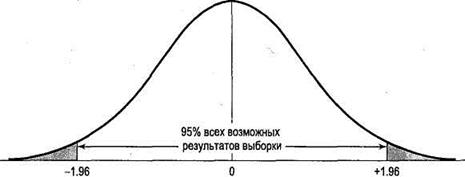
Рис. 7.5. Нахождение стандартизованного значения, соответствующего альфа (а), равной 0,05
Теперь мы знаем, что 95% всех возможных выборочных статистик попадает в диапазон ± 1,96 единиц стандартизованного значения, соответствующего значению генеральной совокупности. В действительности, конечно же, существует только одно значение выборочного показателя, но если мы строим интервальную оценку, основанную на ±1,96 Z, мы получаем вероятность 95% того, что такие интервалы будут включать истинное значение параметра генеральной совокупности. Таким образом, мы можем быть на 95% уверенными в том, что наш интервал включает значение параметра генеральной совокупности.
Помимо доверительного уровня со значением 95%, существует еще три широко используемых значения доверительных уровней: 90% (а = 0,10), 99% (а = 0,01) и 99,9% (а = 0,001). Чтобы найти стандартизованные значения, соответствующие этим уровням, следуйте процедурам, описанным выше для альфа, равной 0,05. В таблице 7.1 приведена вся нужная вам информация.
202 Часть II. Статистические выводы
|
Таблица 7.1. Стандартизованные |
значения для |
различных уровней альфа (а) |
|
|
ДоверительныйуровеньАльфа |
а/2 |
Стандартизованноезначение |
|
|
90% |
0,10 |
0,0500 |
±1,65 |
|
95% |
0,05 |
0,0250 |
±1,96 |
|
99% |
0,01 |
0,0050 |
±2,58 |
|
99,9% |
0,001 |
0,0005 |
±3,29 |
Вам следует обратиться к приложению А и проверить, действительно ли стандартизованные значения из таблицы 7.1 соответствуют этим уровням альфа. При этом обратите внимание на то, что у наблюдений, для которых альфа равна 0,10 и 0,01, точных значений искомой нами площади в таблице нет. Например, если альфа равна 0,10, мы можем обратиться к столбцу С ("Площадь за пределами"), надеясь найти там значение 0,0500. Вместо этого мы видим там значение площади 0,0505 (Z= ±1,64) и значение площади 0,0495 (Z= ±1,65). Искомое нами стандартизованное значение находится где-то между этими двумя значениями. Когда возникает такая ситуация, следует брать большее из двух стандартизованных значений. Это сделает интервал шире при данных обстоятельствах, а потому такой вариант является более осторожным. В случаях, когда альфа равна 0,01, мы сталкиваемся с такой же проблемой (точного значения площади 0,0050 в таблице нет), поэтому нам следует решить ее подобным образом и выбрать большее из значений Z. В конечном итоге, обратите внимание на то, что в случае, когда альфа равна 0,001, мы можем выбрать из нескольких стандартизованных значений. Хотя наша таблица не является достаточно подробной, чтобы это показать, ближайшее стандартизованное значение, соответствующее точному значению нужной нам площади равно ±3,291, что можно округлить до ±3,29. В качестве практического задания, касающегося нахождения стандартизованных значений для различных доверительных уровней, см. задачу 7.3.
Третий шаг заключается в том, чтобы собственно построить доверительный интервал. В последующих разделах мы покажем, как выполнить построение интервальной оценки сначала для выборочных средних, а затем для выборочных пропорций.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.