Экономика и менеджмент \ Статистика

Процедуры оценивания. Смещение и эффективность. Процедуры интервального оценивания выборочных средних, страница 2

'В частности, выборочное стандартное отклонение (s) является смещенной оценкой стандарт­ного отклонения генеральной совокупности (о). Как и следовало ожидать, разброс выборки мень­ше, чем разброс генеральной совокупности, поэтому sбудет меньше, чем а. Однако, как мы уви­дим дальше, в выборочное стандартное отклонение можно внести поправку на это смещение, после чего оно при больших размерах выборки может служить оценкой стандартного отклоне­ния для генеральной совокупности.


198    Часть II. Статистические выводы

ление выборочных статистик — распределение всех возможных значений выбороч­ных показателей, в данном случае, выборочных средних. Таким образом, очень хо­рошей (приблизительно 68 шансов из 100) является вероятность того, что выбороч­ное среднее, равное $35000, находится в пределах ±1 Z, отличной (95 из 100) является вероятность того, что оно находится в пределах ±2 Z, и наилучшей (99 из 100) явля­ется вероятность того, что оно находится в пределах ±3 Z от среднего значения рас­пределения выборочных средних (которое имеет то же значение, что и среднее зна­чение для генеральной совокупности). На рис. 7.1 эти соотношения показаны графически.

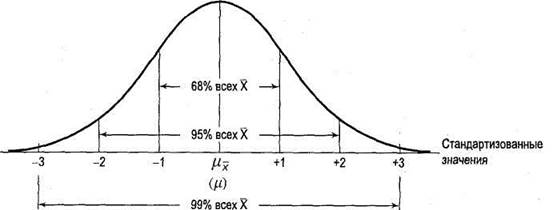
Рис. 7.1. Площади под распределением средних значений выборок

Если статистическая оценка является несмещенной, она, вероятно, представля­ет собой точную оценку параметра генеральной совокупности (в данном случае, /J). Обратите внимание на то, что менее чем для 1% случаев выборочное среднее ока­жется на расстоянии более чем ±3 Z от среднего значения распределения выбороч­ных средних. Мы не имеем ни малейшего понятия, попадает наше выборочное сред­нее, равное $35000, в это меньшинство, или нет. Однако мы знаем, что шансы того, что наше выборочное среднее значительно ближе к среднему значению распределе­ния выборочных средних (т.е. и к среднему значению для генеральной совокупнос­ти), чем ±3 Z, очень высоки.

Второй важнейшей характеристикой статистической оценки является эффектив­ность, выражающая степень группирования выборочного распределения около его среднего. Эффективность или степень группирования по существу связана с разбро­сом. Чем меньше стандартное отклонение распределения выборочных статистик, тем больше степень группирования и выше эффективность. Помните, что стандартное отклонение распределения выборочных средних, или стандартная ошибка средне­го, равно стандартному отклонению для генеральной совокупности, разделенному на квадратный корень из . Таким образом, стандартное отклонение распределения выборочных средних обратно пропорционально N. При увеличении размера выборки будет уменьшаться. Мы можем увеличить эффективность (т.е. уменьшить стандартное отклонение распределения выборочных средних) любой ста­тистической оценки, увеличив размер выборки.


Глава 7. Процедуры оценивания     199

Это можно лучше понять на примере. Рассмотрим две выборки различного раз­мера:

Выборка

1

Выборка 2

 = $35,000

 = $35,000

N1= 100

N2 = 1000

В обеих выборках средние значения являются несмещенными, но у какой из этих статистических оценок больше эффективность? Рассмотрим выборку 1 и предполо­жим, для примера, что стандартное отклонение для генеральной совокупности (о) равно S5002. В данном случае стандартное отклонение распределения всех возмож­ных средних значений выборок, где N равно 100, будет равно , или , или $50. Для выборки 2 стандартное отклонение всех возможных средних значений выборок, где N равно 1000, будет намного меньше. В частности, оно будет равно , или $15,81.

Распределение выборочных средних 2 является более сгруппированным, чем рас­пределение выборочных средних 1. В действительности, распределение 2 содержит 68% всех возможных средних значений выборок в интервале μ ± 15,81, тогда как рас­пределению 1 для этого требуется гораздо более широкий интервал μ ±50,00. Веро­ятность того, что оценка, основанная на выборке, состоящей из 1000 наблюдений, будет близкой по значению к параметру генеральной совокупности, гораздо выше, чем соответствующая вероятность для оценки, основанной на выборке, состоящей из 100 наблюдений. На рис. 7.2 и 7.3 эти соотношения представлены графически.

Скачать файл