Выборочное распределение (распределение выборочных статистик)

Выборочное распределение

(распределение выборочных статистик)

В задачах статистического вывода мы имеем два распределения: 1) эмпирическое распределение, полученное на выборке; 2) распределение генеральной совокупности. Характеристики первого распределения известны (рассчитаны по формулам), второго – неизвестны.

Вывод о распределении генеральной совокупности на основании распределения выборки делается при посредстве важного теоретического механизма – распределения выборочных статистик, или выборочного распределения (sampling distribution). Это центральное понятие теории статистического вывода. Если говорить упрощенно, выборочное распределение говорит нам о том, какие значения конкретной статистики можно ожидать при заданных условиях (например, при условии, что распределение генеральной совокупности имеет параметры μ = 50 и σ = 3). В силу этого своего свойства выборочное распределение позволяет нам оценить вероятность того, что эти заданные условия действительно таковы, как мы полагаем (μ = 50 и σ = 3).

Для более ясного понимания выборочного распределения рассмотрим следующий очень упрощенный пример. Пусть генеральная совокупность состоит из элементов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10. Вы можете убедиться сами, что μ = 5 и σ = 3,32. Случайным образом извлечем из этой генеральной совокупности несколько выборок объемом n = 2 и рассчитаем среднее для каждой выборки. Эту числовую игру можно провести в SPSS, используя правила генерирования случайных значений равномерного распределения и случайных отбор выборок заданного объема. Когда мы выполнили эти операции, в первую выборку попали элементы 6 и 0 (=3), во вторую – 10 и 4 (=7), в третью – 8 и 2 (=5), в четвертую – 0 и 4 (=2), в пятую – 5 и 0 (=2,5). Полученные значения средних являются элементами распределения выборочных средних. Гистограмма этого распределения представлена на рис. 1.

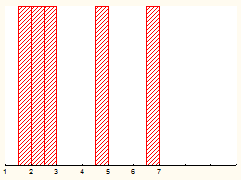
Рис. 1. Распределение средних для пяти выборок, n=2

С увеличением количества и объема выборок распределение выборочных средних начинает приобретать хорошо узнаваемую форму (см. рис. 2).

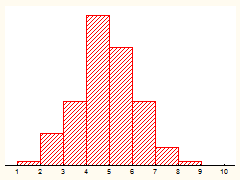
Рис. 2. Распределение средних для 100 выборок, n=2.

Хотя в некоторых специальных случаях выборочные распределения могут строиться подобным образом, эмпирически (методом симуляции процесса извлечения случайных выборок), основные выборочные распределения, которые встретятся вам в распространенных руководствах, были выведены математически.

Выборочное распределение – это теоретическое распределение вероятностей статистик для всех возможных выборок заданного объема (n).Оно включает значения статистик, соответствующие каждой мыслимой комбинации элементов данной генеральной совокупности. Другими словами, распределение выборочных статистик основано на хорошо известных законах теории вероятности, а не на случайной и ненадежной эмпирической информации. Вот почему нам хорошо известны характеристики этого распределения – центральная тенденция, дисперсия, форма.

Вернемся к примеру распределения выборочных средних. Оно обладает следующими важными свойствами:

1. Среднее выборочного распределения средних равно математическому ожиданию (среднему) генеральной совокупности: .

2. Стандартное отклонение выборочного распределения средних меньше стандартного отклонения генеральной совокупности, σ, и зависит от объема выборки. Оно равно . Стандартное отклонение выборочного распределения средних получило специальное название – стандартную ошибку среднего (standard error of a mean)[1].

3. Распределение выборочных средних имеет форму нормального распределения независимо от формы распределения генеральной совокупности.

Эти три свойства, широко используемые в процедурах статистического вывода о неизвестном μ, являются элементами центральной предельной теоремы:

«Если из генеральной совокупности, имеющей распределение любой формы со средним μ и стандартным отклонением σ,многократно извлекать случайные выборки объема n, то при большом nраспределение всех возможных выборочных средних будет стремиться к нормальному распределению со средним μ и стандартным отклонением ».

Трудно переоценить важность этой теоремы для статистического вывода. Во-первых, то обстоятельство, что среднее выборочного распределения средних равно математическому ожиданию генеральной совокупности (как правило, неизвестному), позволяет нам оценить это неизвестное μ.

Во-вторых, поскольку распределение выборочных средних имеет нормальную форму с известным стандартным отклонением, мы получаем возможность оценить вероятность получения разных значений средних (к этому важному свойству мы вернемся в параграфе «Проверка статистических гипотез»).

В-третьих, то обстоятельство, что выборочные средние распределены нормально независимо от формы распределения генеральной совокупности, позволяет эффективно работать даже с теми данными, ненормальность распределения которых хорошо известна (счетные индексы, доход, время реакции). Правда, остается неясным вопрос о том, что означает «большое n». Разные авторы отвечают на этот вопрос по-разному. Одни утверждают, что о нормальной форме распределения выборочных средних необходимы выборки объемом 100 и более. Другие, ссылаясь на результаты компьютерного моделирования, считают достаточно большими выборки объема 30.

Вместо задания.

Воспользуйтесь одной из демонстрационных программ, размещенных в Интернете и посвященных центральной предельной теореме. Убедитесь в том, что математическая статистика занимается простыми, очевидными, понятными и забавными вещами.

http://www.maths.soton.ac.uk/~sml/math1024/links/samplingapplet/SamplingApplet.html – извлекает выборки и разного объема (от 1 до 30 объектов) из трех распределений (нормального, экспоненциального и равномерного). Можно сравнить полученное распределение выборочных средних с распределением генеральной совокупности.

http://www.stat.sc.edu/~west/javahtml/CLT.html – Java-пример с выборками разного объема и разным количеством выборок.

http://www.ruf.rice.edu/~lane/stat_sim/sampling_dist/index.html – особенно эффективная демонстрация с анимацией. Показаны генеральная совокупность, полученное эмпирическое распределение, распределение разных выборочных статистик, в т.ч. среднего, медианы, дисперсии и т.д. Можно, например, убедиться, что среднее распределения выборочных медиан, в отличие от распределения выборочных средних, не совпадает с μ.

http://www.ms.uky.edu/~lancastr/java/cltexp.html

http://faculty.vassar.edu/lowry/VassarStats.html

И т.д.