Рис. 1 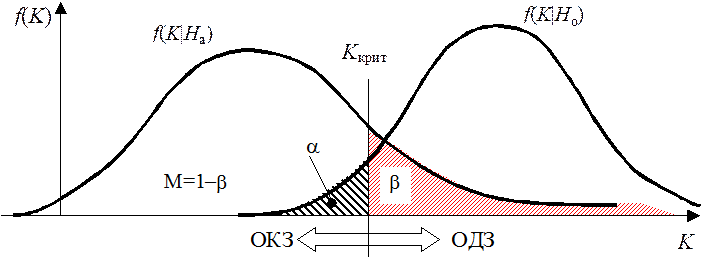
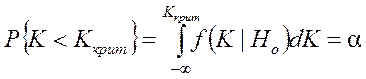 . (1)
. (1)
Рис. 2 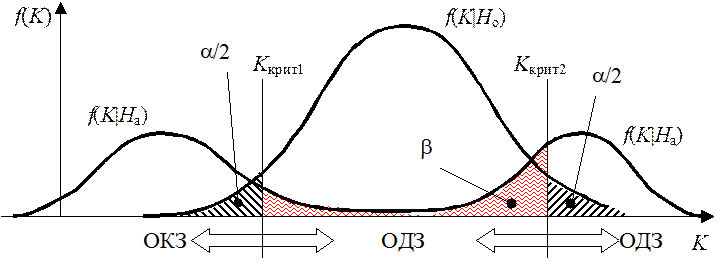
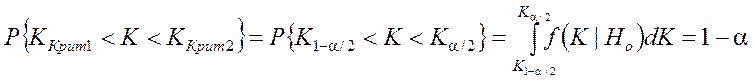 (2)
(2)
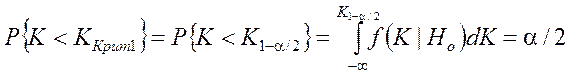 ; (3)
; (3)
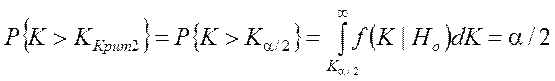 . (4)
. (4)
Алгоритм проверки статистических гипотез с помощью статистических критериев значимости
1. Формулируются гипотезы Ho и Ha , причём гипотеза Ho должна быть простой. Гипотеза Ha принимается в случае, если гипотеза Ho отклоняется.
2. Подбирается статистический критерий значимости K, который (в случае, если Ho верна) имеет заранее известное распределение.
3. Множество возможных значений статистического критерия значимости K разбивается (с учётом гипотезы Ha ) на два непересекающихся множества: область допустимых (ОДЗ) и область критических значений (ОКЗ). Величина ОКЗ статистического критерия выбирается из условия: P{KÎОКЗ|Ho}=a.
4. По результатам n
испытаний определяется выборочное значение статистического критерия значимости ![]() .
.
5. Если KÎОКЗ, то формулируется
вывод: «Ho не согласуется с опытными данными, следовательно, Ho
отклоняется».
Если KÏОКЗ, то формулируется
вывод: «Ho согласуется с опытными данными, следовательно,
оснований для отклонения гипотезы Ho нет».
Проверка гипотезы о
значении МО СВ,
имеющей нормальный закон распределения с известным СКО
Пусть x~N(M[x],s[x]), причём s[x] известно.
1. Требуется проверить гипотезу Ho: M[x]=Ao против Ha: M[x]¹Ao . Ao–const.
2. Рассмотрим величину
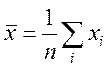 , которая (в силу центральной предельной
теоремы) имеет нормальный закон распределения. M[
, которая (в силу центральной предельной
теоремы) имеет нормальный закон распределения. M[![]() ]=M[x]
]=M[x]
(![]() – несмещённая оценка M[x], т.е.
– несмещённая оценка M[x], т.е. ![]() );
); 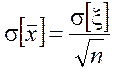 .
.
Для проверки гипотезы Ho
будем использовать статистический критерий значимости 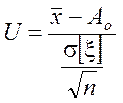 ,
который имеет нормальный закон распределения.
,
который имеет нормальный закон распределения.
Если гипотеза Ho: M[x]=Ao верна, то
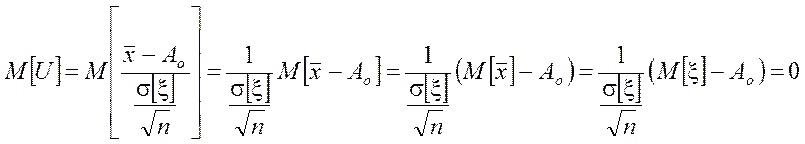 ,
,
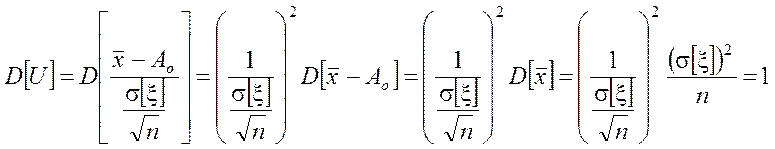 .
.
Таким образом, если Ho верна, то U~N(0,1).
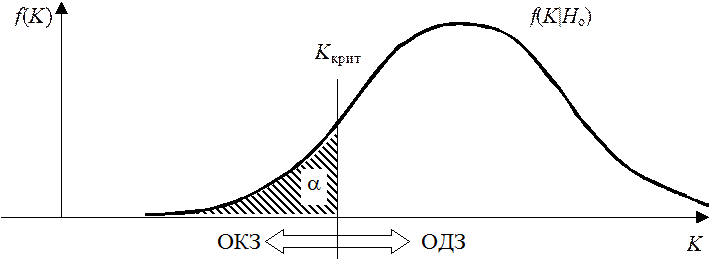
3. В случае, если Ho верна, критерий U наиболее вероятно примет значение близкое к нулю. Если же верна Ha, то СВ U будет принимать очень большие или очень маленькие значения. Таким образом, малые по модулю значения критерия U будем считать допустимыми, а большие по модулю значения – недопустимыми, т.е. критическими (см. рисунок).
|
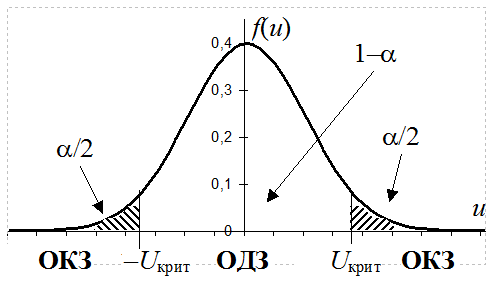
Учитывая симметричность f(u) относительно нуля и то, что ОКЗ – двусторонняя, границы ОКЗ статистического критерия U определяются соотношениями: P{U<–Uкрит|Ho}=a/2; P{U>Uкрит|Ho}=a/2. В последнем выражении, Uкрит=Ua/2 есть квантиль стандартного нормального распределения уровня a/2 (определяется по таблицам).
4. По формуле 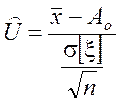 определяется выборочное значение
статистического критерия значимости
определяется выборочное значение
статистического критерия значимости ![]() .
.
5. Если –Ua/2<![]() <Ua/2 , то гипотеза Ho: M[x]=Ao считается
согласующейся с результатами экспериментов (оснований для отклонения гипотезы
нет). В противном случае, гипотеза Ho: M[x]=Ao считается не
согласующейся с результатами экспериментов, она отклоняется в пользу
альтернативной гипотезы; т.е. с вероятностью 1–a можно утверждать, что справедлива гипотеза Ha: M[x]¹Ao . В случае, если |
<Ua/2 , то гипотеза Ho: M[x]=Ao считается
согласующейся с результатами экспериментов (оснований для отклонения гипотезы
нет). В противном случае, гипотеза Ho: M[x]=Ao считается не
согласующейся с результатами экспериментов, она отклоняется в пользу
альтернативной гипотезы; т.е. с вероятностью 1–a можно утверждать, что справедлива гипотеза Ha: M[x]¹Ao . В случае, если |![]() |>Ua/2 , при отклонении
нулевой гипотезы возможно была совершена ошибка 1-го рода, однако вероятность
такой ошибки a»0.
|>Ua/2 , при отклонении
нулевой гипотезы возможно была совершена ошибка 1-го рода, однако вероятность
такой ошибки a»0.
ПРИМЕЧАНИЕ: Если требуется проверить гипотезу Ho: M[x]=Ao против Ha: M[x]>Ao или против Ha: M[x]<Ao пп. 1,3,5 алгоритма модифицируются.
1-а. Ho: M[x]=Ao против Ha: M[x]>Ao .
3-а. Если Ho верна, то критерий наиболее вероятно U=0. Если же верна Ha: M[x]>Ao, то U будет принимать большие положительные значения. ОКЗ определим как множество значений, характерных для критерия U в случае справедливости гипотезы Ha. Величина ОКЗ определяется из условия P{UÎОКЗ|Ho}=a Þ P{U>Uкрит|Ho}=a Þ P{U>Ua|Ho}=a, где Ua – квантиль стандартного нормального распределения уровня a (определяется по таблицам).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.