Статистическая проверка параметрических гипотез, страница 7

Пусть x~N(M[x],s[x]), h~N(M[h],s[h]), параметры s[x]=s[h] неизвестны.

1. Требуется проверить гипотезу H_o: M[x]=M[h] против H_a: M[x]¹M[h]. Другими словами, следует установить: значимо или незначимо различаются  и .

2. Для проверки гипотезы H_o: M[x]=M[h] относительно равенства МО двух независимых СВ, имеющих нормальные законы распределения с неизвестными, но равными СКО, используется статистический критерий значимости 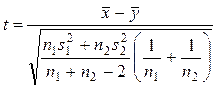, который (в случае, если H_o верна) имеет распределение Стьюдента с n=n₁+n₂–2 степенями свободы, т.е. t~t(n₁+n₂–2). Здесь n₁ и n₂ – объёмы выборок СВ x и h; s₁ и s₂ – значения несмещённых оценок СКО СВ x и h.

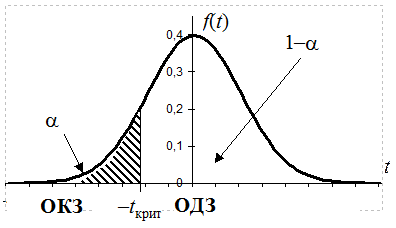
3. В случае, если H_o верна, критерий t наиболее вероятно примет значение близкое к нулю. Если же верна H_a, то СВ t будет принимать очень большие или очень маленькие значения. На множестве возможных значений статистического критерия t определим ОКЗ, которые являются характерными для критерия t в случае справедливости альтернативной гипотезы. Величину ОКЗ определим из условия P{tÎОКЗ|H_o}=a. Учитывая симметричность f(t) относительно нуля, критические значения статистического критерия t определяются соотношением: t_крит=t_{a/2, n1+n2-2} , где t_{a/2, n1+n2–2}  – квантиль распределения Стьюдента уровня a/2 с n=n₁+n₂–2 степенями свободы (определяется по таблицам).

Рисунок 13.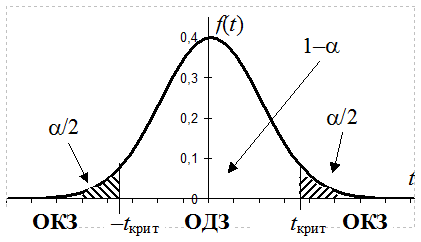

4. По формуле 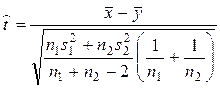 определяется выборочное значение статистического критерия значимости .

5. Если – t_{a/2, n1+n2–2}<<t_{a/2, n1+n2–2} , то гипотеза H_o: M[x]=M[h] считается согласующейся с результатами экспериментов (оснований для отклонения гипотезы нет). В противном случае, гипотеза H_o: M[x]=M[h] считается не согласующейся с результатами экспериментов, она отклоняется в пользу альтернативной гипотезы; т.е. с вероятностью 1–a можно утверждать, что справедлива гипотеза H_a: M[x]¹M[h]. В случае, если ||>t_{a/2, n1+n2–2} , при отклонении нулевой гипотезы возможно была совершена ошибка 1-го рода, однако вероятность такой ошибки a»0.

Примечание. В случае, если требуется проверить гипотезу H_o: M[x]=M[h] против H_a: M[x]<M[h] или H_a: M[x]>M[h]  ОКЗ для этих случаев выглядят следующим образом.

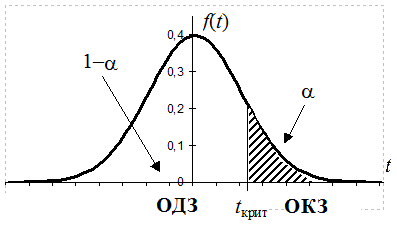
H_o: M[x]=M[h] ; H_a: M[x]>M[h]                                        H_o: M[x]=A_o ; H_a: M[x]<M[h]

Рисунок 14.                                                     Рисунок 15.

Послесловие

На двух данных лекциях мы определились с основными понятиями и идеей проверки статистических гипотез с помощью статистических критериев. Определили ошибки, возможные при проверке статистических гипотез. Еще мы узнали, что если одна из гипотез (нулевая или альтернативная) является сложной, то распределение статистического критерия, используемого при проверке гипотезы, не является определённым. Следовательно, невозможно точно определить вероятность совершения одной из двух ошибок, совершаемых при проверке гипотезы.

На данных лекциях мы подробно рассмотрели методики проверки 4-х типов параметрических гипотез. В двух случаях даже сами обосновали применение того или иного статистического критерия значимости. В двух других случаях мы воспользовались статистическими критериями, рекомендуемыми фундаментальной литературой по МС.

Вообще-то следует заметить, что идея проверки статистических параметрических гипотез тождественна идее построения доверительных интервалов для исследуемых параметров распределения СВ и проверки на принадлежность гипотетического значения найденному доверительному интервалу (или полуинтервалу).

На следующей лекции мы рассмотрим пример построения доверительного интервала, а также проверки одной параметрической гипотезы, сделаем предметные выводы. Кроме того, мы рассмотрим две методики проверки непараметрических гипотез, в которых (напомню) формулируются предположения о виде функций распределения случайных величин.