Статистическая проверка параметрических гипотез, страница 3

Разделим область возможных значений СВ K на две непересекающиеся обрасти (область допустимых значений – ОДЗ и область критических значений – ОКЗ) (см. рисунок 1) таким образом, чтобы в случае справедливости нулевой (а не альтернативной гипотезы), вероятность попадания СВ K в ОКЗ была равна некоторому заранее фиксированному значению a, а вероятность попадания в ОДЗ соответственно равна  1–a (см. рисунок 1).

Рисунок 1.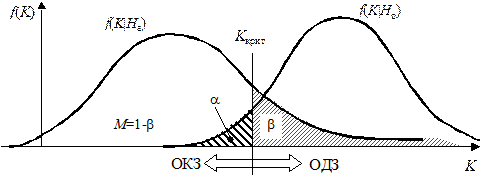

Если известно, что M[K|H_o]>M[K|H_a] (см. рисунок 1), то граничное значение статистического критерия определяется из условия:

.

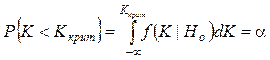Рисунок 2.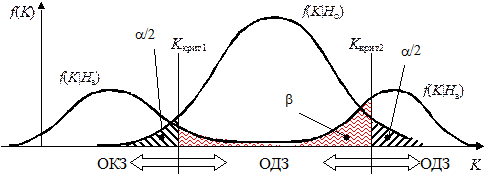

Если функции плотности распределения статистического критерия в случае верности нулевой или альтернативной гипотезы имеют вид, представленный на рисунке 2, то граничные значения статистического критерия определяются из условия:

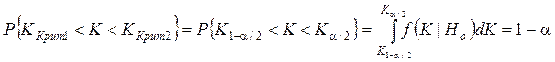
или условий

;

.

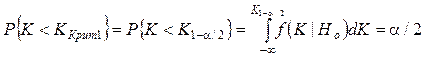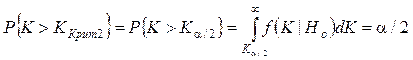Расположение ОКЗ по отношению к ОДЗ статистического критерия зависит в основном от характера альтернативной гипотезы и может быть односторонним (правосторонним или левосторонним, как на рисунке 1) или двусторонним, как на рисунке 2.

Итак, в случае, если нулевая гипотеза верна, вероятность того, что значение статистического критерия K не попадет в ОДЗ, равна a. Зададим вероятность a очень малой, чтобы попадание СВ K в ОКЗ можно было считать практически невозможным событием. Тогда, если нулевая гипотеза справедлива, то при её проверке наблюдаемое (выборочное) значение статистического критерия K должно обязательно попасть в ОДЗ. Если же наблюдаемое значение критерия попадает в ОКЗ, то произойдет практически невозможное событие. И можно считать, что с вероятностью (1–a)»1 проверяемая нулевая гипотеза несправедлива.

Проиллюстрируем идею проверки статистических гипотез и дадим геометрическую интерпретацию вероятностей ошибок 1-го и 2-го рода, а также мощности статистического критерия, который имеет левостороннюю критическую область.

Пусть в случае, если верна нулевая гипотеза, функция плотности статистического критерия имеет вид f(K|H_o), а в случае, если H_o не верна (верна H_a) функция плотности статистического критерия имеет вид f(K|H_a) (см. рисунок 1). Для заданной альтернативной гипотезы и уровня значимости выбирается ОКЗ и ОДЗ статистического критерия K.

Выбор значения a зависит от потерь, вызываемых ошибками 1-го и 2-го рода. Так, если совершение ошибки 1-го рода приведет к большим потерям, чем ошибка 2-го рода, то следует уменьшить a. Но, на сколько следует уменьшить a всегда вопрос открытый, и решается индивидуально для каждого отдельного случая. Обычно в инженерных расчётах a=0,05; в медицинских расчётах a=0,01. При исследовании безопасности технических средств a=0,005. Хотя многое зависит от выдвигаемой гипотезы H_o и того вывода, который может быть сделан.

Вопрос: как изменится вероятность совершения ошибки 1-го рода при изменении вероятности ошибки 2-го рода? Как это отразится на мощности статистического критерия?

К сожалению, на практике, при проверке статистических гипотез одна из гипотез (обычно – альтернативная) часто является сложной. А поскольку такая гипотеза содержит в себе множество предположений, то в этом случае принципиально невозможно знать распределение статистического критерия. А значит невозможно однозначно контролировать ошибку первого или второго рода (или обе ошибки, если обе гипотезы являются сложными).

Поэтому на практике при проверке статистических гипотез обычно стараются, чтобы нулевая гипотеза была простой, а сложной была альтернативная гипотеза. В этом случае ограничиваются учётом информации лишь об ошибке 1-го рода.

Вот и мы будем рассматривать только один вид статистических критериев – статистические критерии значимости, при применении которых вероятность a фиксирована заранее и не учитывается вероятность b. Т.е. на основании применения статистических критериев значимости с заранее фиксированным риском принимается лишь одно из двух решений: «нулевая гипотеза не согласуется с результатами эксперимента, поэтому H_o отклоняется» или «нулевая гипотеза согласуется с результатами эксперимента, поэтому нет оснований для отклонения H_o». Следует подчеркнуть, что статистические критерии значимости не позволяют принимать решений о том, что «H_o является верной и она принимается», поскольку статистические критерии значимости не контролируют ошибку 2-го рода.