Дискретная математика: Учебное пособие. Часть I - Основания дискретной математики, страница 5

h: Xⁿ®Y, где h -оператор отображения.

Мощность отображения не больше мощности прямого произведения, т.е.

 |H|£|X₁|_*|X₂|_*.._*|X_n|_*|Y|.

Каждому отображению h может быть найдено обратное отображение:

h^-1: Y¬Xⁿ.

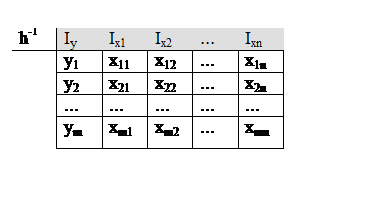H^-1={(y, x₁, x₂,..x_n)| x_iÎX, yÎY}Í(YÄXⁿ).

Обратное отображение удобно применять для формирования таблиц реляционных баз данных, когда в “шапке” таблицы указывают имя соответствующей компоненты - I_y, I_x1, I_x2,..I_xn, а в “теле” записывают значения соответствующих компонент. Строка таблицы называется записью (record), а столбец – полем (field). Такую таблицу называют отношением.

Ниже дан фрагмента отношения: “Журнал заказов..”. В первом столбце дан уникальный код заказа (I_y), который называют ключом для всей записи, а в остальных столбцах указаны атрибуты заказа: I_x1 – клиент заказа, I_x2 – дата заказа, I_x3 – адрес клиента, I_x4 – город клиента, I_x5 – индекс города, I_x6 – страна, в которой проживает клиент.

Понятие отображение логически совпадает с понятием функция, т.е.

f=(x, y) или f=(x₁, x₂,..,x_n,  y).

Например, f₊=(x₁, x₂, y) есть y=x₁+x₂,

f_exp=(x₁, x₂, y) есть y=x₁^x2,

f_sg=(x, y) есть y=sg(x).

В этом случае элементы х и (x₁, x₂,..,x_n) называют аргументами, а y –значением функции f(x₁, x₂,..,x_n).

Множество, связывающее заданные аргументы и определяемые значения функции, называют графиком функции.

Например, множества f={(a, b)| aÎA, bÎB}Í(AÄB) или

f={(a₁, a₂,..,a_n, b)| a_iÎX; bÎY}ÍXⁿÄY есть графики соответствующих функций.

Частным случаем является функция, принимающая значение на двухэлементном множестве {“истина”, “ложь”} или {1, 0}. Такая функция называется логической или предикатом. В тексте ее обозначают Р(х) или Р(x₁, x₂,..,x_n). Эта функция по заданному условию (или характеристическому свойству) позволяет формировать новые множества.

Например, если на множестве целых чисел заданы предикаты:

Р₁(х):-”x - простое число”;

Р₂(x_i, x_j):- ”x_i и x_j имеют общий делитель”

Р₃(f₊(x_i, x_j), x_k):- ”x_k ,больше суммы x_i и х_j”,

то для x₁=3, х₂=4 и х₃=8 будут получены следующие результаты:

Р₁(3)=“истина”; Р₁(4)=“ложь”; Р₁(8)=“ложь”;

Р₂(3, 4)=“ложь”; Р₂(3, 8)=“ложь”; Р₂(4, 8)=“истина”;

Р₃(f₊(3, 4), 8)=“истина”;

Если эти предикаты задать на конечном множестве чисел {1, 2,..10}, то будут сформированы графики: X₁={x| Р₁(х)}= {2, 3, 5, 7}, X₂= {(x_i, x_j)| Р₂(x_i; x_j)}=

{(2, 4), (2, 6), (2, 8), (3, 6), (3, 9),.. (8, 10)}, X₃= {(f₊(x_i, x_j), x_k)| Р₃(f₊(x_i; x_j); x_k)}={(1, 2, 4), (1, 2, 4),..(2, 3, 5),..(8, 1, 10) }.                                                                          

Логические функции также удобно представлять таблицами, позиции которой содержат символ “1” если выполняется логическое условие и “0” в противном случае. Например, таблица справа описывает множество наборов x_i и x_j, для которых выполняется логическое условие Р₂(x_i, x_j) для Z={1,2,..10}. Следует еще раз обратить внимание, что в таблице представлены совместимые кортежи для каждого x_i, т.е. в формировании логической функции участвуют все аргументы со значением “1” или “0”.

1.  3 Отношение