Математика \ Дискретная математика

Дискретная математика: Учебное пособие. Часть I - Основания дискретной математики, страница 12

Симметрическая разность множеств А и В есть множество, состоящее из всех тех элементов, которые принадлежат разности (А\В) или (В\А).

 Симметрическую разность множеств (“D”) также можно исполнить, опираясь только на основные операции объединения, пересечения и дополнения по правилу: С=(АDВ)=(АÇùВ)È(ВÇùА)={x|xÎ(A\В) или xÎ(B\А)}.

Операторная запись имеет вид: С:=union(difference(A, B), difference(B, A)).

Следует обратить внимание, что если (АDВ)=(АÇùВ)È(ВÇùА)=Æ, то А=В. Это правило будет часто использоваться при доказательстве тождеств и поиске неизвестных множеств.

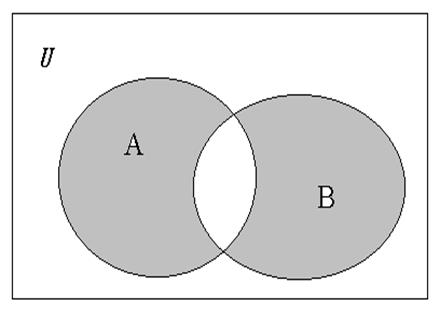
Рис.6 Симметрическая разность множеств A и B.

Пример: Пусть даны множества A={a, b, c}, B={b, c, d, e}. Найти C= (АDВ).

C={a, d, e}, т.к. элементы b, сÎA, B.

Пример: Пусть даны множества A и B, которым принадлежат подмножества A={{a, b}, c}, B={{b, c, d}, c, d}. Найти C= (АDВ).

C={{a, b}, {b, c, d}, d} т.к. элемент сÎA, B.

          Пример: Пусть даны множества несовместимых кортежей A={(a,b), (b, c)}, B={(b, c), (b, c, d), (c, d)}. Найти C= (АDВ).

C={(a, b), (b, c, d), (c, d)}, т. к. кортеж (b, c)ÎA, B.

Пример: Пусть даны отображения h1 и h2, представляющие множества совместимых кортежей. Найти h=(h1Dh2).

h1

y

x1

x2

x3

D

h2

y

x1

x2

x3

=

h=(h1Dh2)

y

x1

x2

x3

2

b

c

6

3

c

e

2

2

b

c

6

3

c

e

5

5

c

b

2

3

c

e

5

5

c

b

2

4

a

e

5

3

c

e

2

4

a

e

5

2

a

e

6

2

a

e

6

В таблицу h не вошли кортежи (5, c, b, 2) и (4, a, e, 5)}, которые принадлежат h1 и h2.

Пример: Пусть даны отношения r1 и r2. Найти r=(r1Dr2).

Особенность исполнения этой операции состоит в том, что
операция r=(r1Dr2) выполняется для каждой пары (xi, xj), входящей в r1 и r2, по правилу:


r(xi, xj)=(r1(xi, xj) ×`r2(xi, xj))Úr2(xi, xj) ×`r1(xi, xj).

r1

x1

x2

x3

x4

r2

x1

x2

x3

x4

r=(r1Dr2)

x1

x2

x3

x4

x1

1

0

0

0

x1

0

1

1

1

x1

1

1

1

1

x2

0

1

0

1

D

x2

1

1

0

0

=

x2

1

0

0

1

x3

1

0

1

0

x3

0

1

1

0

x3

1

1

0

0

x4

0

1

1

1

x4

0

0

0

0

x4

0

1

1

1

1.6 Операции над множествами

Формулы алгебры множеств. Выражение, компонентами которого являются элементы носителя алгебры множеств и символы алгебраических операций, называют формулой F.

Множества A, B, С,.. называют элементарными формулами.

Выражения F=ùA, F=(AÈB), F=(AÇB), F=(AÈС), F=(AÇС), F=(BÈC), F=(BÇC) называют формулами первого порядка, а выражения ùF, (F1ÈF2), (F1ÇF2) – второго и более высоких порядков.

 Никаких иных формул в алгебре множеств нет.

Скачать файл