Дискретная математика: Учебное пособие. Часть I - Основания дискретной математики, страница 4

Если по какому-либо правилу для элементов множества A ставится в соответствие один или несколько элементов множества B, то формируется множество упорядоченных пар {(x, y)| xÎA, yÎB}. Тогда множество A называют областью отправления, а множество B - областью прибытия.

Например, в  таблице область отправления есть атрибуты <дата_рожд.>, <дом_адрес>, <дом_тел.>, а область прибытия -<фамилия>, <имя>.

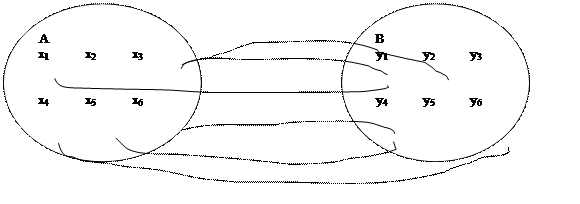Рис. 1 Отображение элементов множества A на множество B.

Каждая строка таблицы есть кортеж, который в базах данных называют записью (record), а компоненту кортежа – полем записи (field).

На рис. 1 показаны области отправления A={x₁, x₂,..x₆} и прибытия –

B={y₁, y₂,..y₆} для пар {(xi, yj)| xiÎA, yjÎB}. Проекция на первую компоненту пары p₁{(x, y)} формирует область определения A₀={x₁, x₃, x₄, x₅, x₆}ÍA, а на вторую компоненту p₂{(x, y)} - область значений B₀={y₁, y₂, y₄, y₆}ÍB. Элементы y_jÎB₀  называют образом элемента х_iÎA₀, а элемент х_iÎA₀ - прообразом элемента y_jÎB₀.

Например, на рис.1 образом для x₁ является y₁, для x₂ - Æ, для x₃ – {y₁, y₂}, для x₄ - y₆, для x₅ – y₄, для x₆ – y₄, прообразом для y₁ – {x₁, x₃}, для y₂ – x₃, для y₃=Æ, для y₄ – {x₅, x₆}, для y₅ - Æ, для y₆ – x₄.

Если для одного или нескольких элементов х_iÎA⁰ существует несколько образов, т.е. |{y}_xi |>1, то такое множество упорядоченных пар называют соответствием.

Например, на рис. 1 имеем для x₃ – {y₁, y₂}.

Соответствие представляют, как правило, двуязычные словари, когда слову одного языка, как правило, соответствует несколько слов другого языка:

capacity – способность, мощность, емкость,

array – массив, таблица, расположение,

 scanner - лексический анализатор, устройство для ввода изображений и др..

Если для каждого элемента х_iÎA⁰ существует единственный образ, т.е.

 |{y}_xi |=1, то такое множество упорядоченных пар называют отображением.

Например, в компьютере каждая буква, цифра или символ отображаются в уникальную 8-битовую кодовую комбинацию: “F”:=01000110,.. “s”:=01110011,.. ”Ф”:=11000100,.. “я”:=11001111,.. “5”:=00110101,.. “+”:=00101011,.. “&”:=00100110,.. “{“:=01111011 и т.д.

Очевидно, что каждое отображение h=(x, y) есть кортеж, а их множество есть подмножество прямого произведения множеств A и B, т.е.

H={(x, y)|xÎA, yÎB}Í(AÄB).

Если область определения задана на нескольких множествах Х_i, то

h=(x₁, x₂,..,x_n, y), а H={(x₁, x₂, ..,x_n, y)|x_iÎX_i, yÎY}Í((X₁ÄX₂Ä..ÄX_n)ÄY).

В этом случае y_jÎY⁰ является образом для (x_1i, x_2i,..,x_ni)Î(X₁ÄX₂Ä..ÄX_n), а

(x_1i, x_2i,..,x_ni)Î(X₁ÄX₂Ä..ÄX_n) - прообразом для y_jÎY⁰.

Если X₁=X₂=..=X_n=X, то H={(x₁, x₂,..,x_n, y)|x_iÎX, yÎY}Í(XⁿÄY).

Отображения удобно описывать таблицами.

Например, все кодовые комбинации, замещающие в компьютере буквы, цифры и символы удобно сгруппировать в таблицы.

Отображения (x; y) и (x₁, x₂,..,x_n, y) представляют кортежи, заданные на множествах (XⁿÄY). Для n=1 отображение называют унарным, для n=2 - бинарным, для n=n – n-арным отображением

Отображение удобно представлять в операторной форме: