Дискретная математика: Учебное пособие. Часть I - Основания дискретной математики, страница 10

Если В=Æ, то АÇВ=АÇÆ=Æ.

Если B=U, то АÇВ=АÇU=А.

Рис. 3 Пересечение множеств A и B.     Если СÍА и СÍВ, то СÍАÇВ. Если А¹Æ и В¹Æ, то при АÇВ=Æ множества A и B не имеют общих элементов.

Пример: Пусть A={a, b, c}, B={b, c, d, e}. Найти C= (АÇВ).

 C={b, c}, т. к. b, cÎA и B.

Пример: Пусть даны множества A и B, которым принадлежат подмножества A={{a, b}, c}, B={{b, c, d}, c, d}. Найти C= (АÇВ).

C={c}, т. к. {a, b}ÏB и {b, c, d}, dÏA.

          Пример: Пусть даны множества несовместимых кортежей A={(a, b), (b, c)}, B={(b, c), (b, c, d), (c, d)}. Найти C= (АÇВ).

C={(b, c)}, т. к. кортежи (a, b)ÏB, (b, c, d), (с, d)ÏA.

Пример: Пусть даны отображения h¹ и h², представляющие множества совместимых кортежей. Найти h=(h¹Çh²).

Если все компоненты двух совместимых кортежей имеют одинаковые значения, т.е. (y⁽¹⁾=y⁽²⁾;x₁⁽¹⁾=x₁⁽²⁾;x₂⁽¹⁾=x₂⁽²⁾;...x_n⁽¹⁾=x_n⁽²⁾), то в результате исполнения этой операции формируется один кортеж (y;x₁;x₂;...x_n), при различии хотя бы одной компоненты совместимых кортежей в результате исполнения этой операции формируются пустой кортеж.

В h войдут только кортежи (5, c, b, 2), (4, a, e, 5), которые принадлежат h¹ и h².

h1

y

x1

x2

x3

Ç

h2

y

x1

x2

x3

h=(h1Çh2)

y

x1

x2

x3

2

b

c

6

3

c

e

2

=

5

c

b

2

3

c

e

5

5

c

b

2

4

a

e

5

5

c

b

2

4

a

e

5

4

a

e

5

2

a

e

6

Пример: Пусть даны отношения r¹ и r². Найти r=(r¹Çr²).

Операция r=(r¹Çr²) выполняется для каждой пары (x_i, x_j), входящей в r¹ и r², по правилу конъюнкции: r(x_i, x_j)=r¹(x_i, x_j)×r²(x_i, x_j).

r1	x1	x2	x3	x4		r2	x1	x2	x3	x4		r=(r1Çr2)		x1	x2	x3	x4
x1	1	0	0	0		x1	1	1	1	1			x1	1	0	0	0
x2	0	1	0	1	Ç	x2	1	1	0	0	=		x2	0	1	0	0
x3	1	0	1	0		x3	0	1	1	0			x3	0	0	1	0
x4	0	1	1	1		x4	0	0	0	1			x4	0	0	0	1

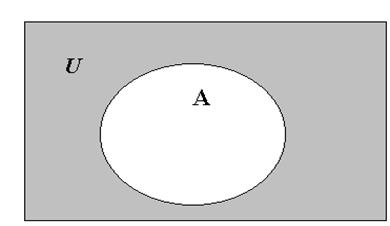Дополнение множества А есть множество, состоящее из всех тех элементов, которые принадлежат универсальному множеству U и не принадлежат множеству А, т.е.ùА={x| xÎU и xÏA}.    

Операторная запись дополнения имеет вид: ùА=complement(A).

Если существуетùА, то справедливы следующие соотношения: АÇùА=Æ, АÈùА=U и ù(ùА)=А.

Рис.4 Дополнение множества А

Пример: Пусть дано множество A={a, b, c}и универсальное множество U={a, b, c, d, e, f}. Найти C=ùА. C={d, e, f}.

Пример: Пусть дано множество A={{a, b}, c} и универсальное множество U={a, b, {a, b}, c, {d, e}, f}. Найти C=ùА.

C={a, b, {d, e}, f}.

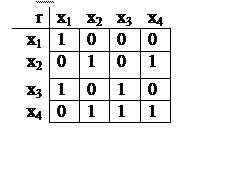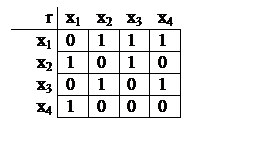Пример: Пусть дано отношение r. Найти `r.