Дискретная математика: Учебное пособие. Часть I - Основания дискретной математики, страница 11

Особенность исполнения этой операции состоит в том, что значения r(x_i; x_j) также принадлежат двухэлементному множеству {0; 1}. Поэтому для r(x_i;x_j)=1 значение r(x_i;x_j)=0, а для r(x_i;x_j)=0 значение`r(x_i;x_j)=1.

Пример: Пусть дано отображение h.

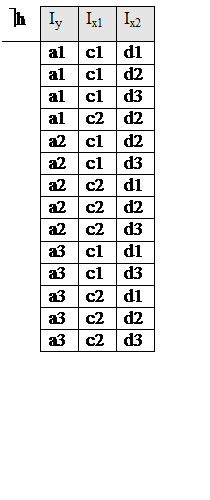
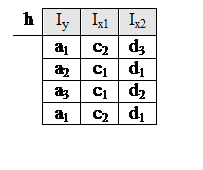Для поиска ùh необходимо найти множество кортежей, совместимых с кортежами h, но отличающихся значением хотя бы одной компонентой. Для этого определяют число элементов n  области определения h  и число компонент k.

Тогда |ùh|=n×(n-1)×(n-2)×..×(n-k+1) -|h|.

Для h, представленной на таблице, имеем n=|I_y|+|I_x1|+|I_x2|=3+2+3=8 и k=3. Тогда |ùh|=8×7×6 – 4 =332,

 т. е. таблица  ùh должна содержить 332 кортежа. Однако, если принять, что значения компонент кортежей не выходят за пределы своего атрибута, т. е. |I_y|=3, |I_x1|=2, |I_x2|=3, то |ùh |=3×2×3 – 4=14.

          Пример: Пусть дано множество кортежей A={(a,b),

(b, c)} и универсальное множество U={(b, c), (b, c, d), (c, d), (a,b)}. Найти C=ùА.

C={(b, c, d,), (c, d)}.

Операции дополнения, пересечения и объединения формируют две дополнительные операции: разности и симметрической разности.

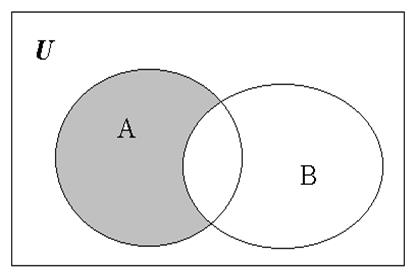Разность множеств А и В есть множество, состоящее из всех тех элементов, которые принадлежат множеству А и не принадлежат множеству В, т.е.

С=(А\В)= {x|xÎА и xÏВ}, где “\” - символ разности.

Операторная запись разности имеет вид: С=difference(A, B).                                        Рис. 5 Разность множеств A и B.

Исполнение этой операции можно реализовать с помощью основных операций конъюнкции множества A с дополнением множества B,

 т. е.С=(А\В)=(АÇ(ùВ)).

Пример: Пусть даны множества A={a, b, c}, B={b, c, d, e}. Найти C= (А\В).

C={a}, т.к. элементы b, сÎB.

Пример: Пусть даны множества A и B, которым принадлежат подмножества A={{a, b}, c}, B={{b, c, d}, c, d}. Найти C= (А\В).

C={a, b}, т.к. элемент сÎB.     

Пример: Пусть даны множества несовместимых кортежей A={(a,b), (b, c)}, B={(b, c), (b, c, d), (c, d)}. Найти C= (АÈВ).

C={(a, b)}, т. к. кортеж (b, c)ÎB.

Пример: Пусть даны отображения h₁ и h₂. Найти h=(h₁\h₂).

Если для совместимых кортежей двух отображений есть различие хотя бы одной компоненты, то записывается кортеж первого отображения.

Пример: Пусть даны отношения r₁ и r₂. Найти r=(r₁\r₂).

Особенность исполнения этой операции состоит в том, что
операция r=(r₁\r₂) выполняется для каждой пары (x_i, x_j), входящей в r₁ и r₂, по правилу конъюнкции r₁(x_i, x_j) и `r<sub>2</sub>(x<sub>i</sub>, x<sub>j</sub>), т. е.
 r(x<sub>i</sub>, x<sub>j</sub>)=(r<sub>1</sub>(x<sub>i</sub>, x<sub>j</sub>)×`r₂(x_i, x_j)).