Теория электромагнитного поля. Закон Кулона. Теорема Гаусса в интегральной форме, страница 9

                                         

(***)-3-я форма записи формул Максвелла.

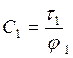  => >0
Все собственные частичные емкости – положительны. 3-й гр. формул Максвелла соотв. схема с частичной емкости.

  Согласно системе 3 – полный заряд к-того провода равен сумме отдельных составляющих: сост. заряда   обусловл. разностью потенциалов м-у к-тым проводом и землей, а составл. Заряда  обусловлено разностью потенциалов м-у к-тым и м-ным проводами, отсюда ясно, что собстсв. частичная ёмкость  может рассматриваться как отношение «поруки» заряда к-того провода, обусловленной разностью потенциалов м-у к-тым проводом и землей к величине этой разности потенциалов. Соответственно взаимную частичную ёмкость  можно рассматривать как отношение «поруки» заряда к-того провода обусловленной разностью потенциалов м-у к-тым и м-ным проводами к величине этой разности.

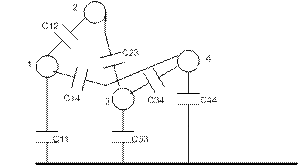
  Ёмкость двухпрводной линии передачи с учетом влияния земли.

r – радиус проводов

D – расстояние м-у ними

а -  высота подвеса

Воспользуемся 1 группой формул Максвелла.

                                      

;

;

,

.

.

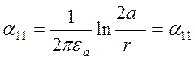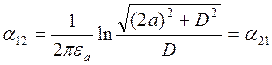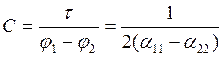   Ёмкость линии перез. На единицу длинны с учетом земли.

,

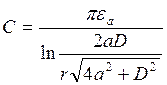        если а >> D                                .

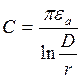   Если высота подвеса проводов много больше расстояния м-у ними, то исчезает влияние земли на ёмкость двух проводов линии передачи:

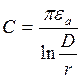 - результат получ. ранее без учета влияния земли.

Ротор (вихрь)

Дифферен. форма условия потенциальности электростат-го поля.

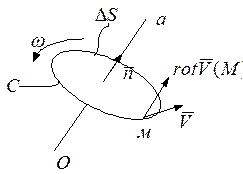
Пусть в некоторой области пространства происходит вращение его точек с постоянной угловой скоростью вокруг оси ОА , направление которой определяется единичным вектором. Выберем для примера траекторию С- окружности, тогда вектор  одновременно является нормалью к площадке , ограниченной траекторией. Вектор линейной скорости  в любой точке траектории вращения по касательной к траектории. Назовем ротором (вихрем) вектора  в точке м вектор rot (м) совподающий по напровлению с напровлением оси вращения. Длина указанного вектора в рассмот-ом примере:                              

                    

Окончательно можем записать: 

Выражение () физический смысл ротора—он характеризует вращательное движение в поле векторов  .

Действительно ,если есть вращение-- (иначе есть замкнутая траектория вектора ) –есть ротор вектора ; нет вращения (линии вектора разомкнуты)—нет ротора.

В общем случае (для произвольного поля векторов ) ,, rot-связаны соотношением  nrot =rot_n=Cim

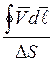
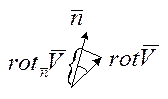
  проекция ротора вектора  на нормаль
Правая часть есть предел отношение циркуляции вектора   по замкнутому контуру к площади, ограниченной этим контуром при условии стремления последней к нулю.

Выше условие потенциальности электростатического поля было записано в интегральной форме 

Отсюда  rot

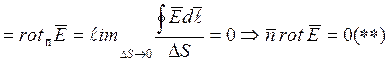
Поскольку выр-е (**) справедливо для любого замкнутого контура, а  для любого направления нормали , то  (***)—диффер-я форма условия потенциальности элекростатич--го  поля.

Выражение(***) свид—ет о том, что лнии вектора (силовые линии) не замыкаются сами на себя (не образуют вихрей), а имеют нач. и конец. Потенц. поле и вихревое – одно и то же.

Элекрическое поле постоянного тока в проводящей среде. 

При протекании пост. тока как внутри проводящего тела, так и вне его сущ—ет постоянное магнитное поле. Поскольку оно не изменно во времени, то не возникает явление ЭМИ. (т. е. магнит. Поле, созданное пос. токами не оказывает влияние на электрич-е поле того же тока). Поэтому элект-е и магн-е поля можно рассмат. (изучать) раздельно.                                       

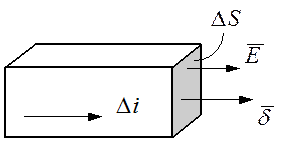  Плотность тока и ток.        

 Упорядоченное перемещение свободных носителей электрических зарядов в проводнике под воздействием электрического поля называется током проводимости.

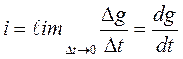
  Мерой  направленного движения зарядов служит вектор плотности тока , онсовподает по направлению с вектором  и численно определяется как                                                                                                                       

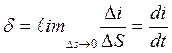                                         Отсюда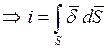

Ток ч/з поверхность S равен потоку вектора плотности тока ч/з туже поверхность.