Проведем ч/з данную точку цилиндрическую поверхность так, чтобы ось цилиндра совпадала с заряженной осью.
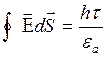
2-я форма записи т. Гаусса в дифф. форме записи.
Поток вектора ![]() ч/з донышки цилиндра = 0, т.к.
ч/з донышки цилиндра = 0, т.к. ![]()
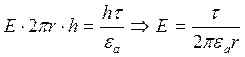 или в
векторной форме
или в
векторной форме 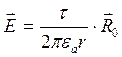 .
.
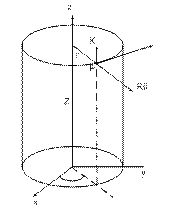 Для определения
потенциала выберем цилиндрическую С.К. В этом случае эквипотенциальная
поверхность поля совпадает с выбранной координатной поверхностью.
Для определения
потенциала выберем цилиндрическую С.К. В этом случае эквипотенциальная
поверхность поля совпадает с выбранной координатной поверхностью.
В Ц.С.К. положение точки Р
характеризуется тремя координатами ![]() , а выражение для grad имеет вид:
, а выражение для grad имеет вид:
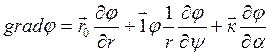 .
.
Очевидно, что в этом случае
потенциал рассматриваемой точки зависит только от одной координаты ![]() и выражение для grad упрощается
и выражение для grad упрощается
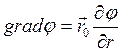
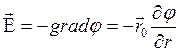 или
для модулей
или
для модулей 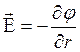 , откуда
, откуда 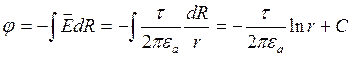 .
.
Величина постоянной интегрирования зависит от того, потенциал какой точки принимается равным 0.
Пример(Метод наложения):
Определить ![]() и Е поля, создаваемого двумя заряженными
осями.
и Е поля, создаваемого двумя заряженными
осями.
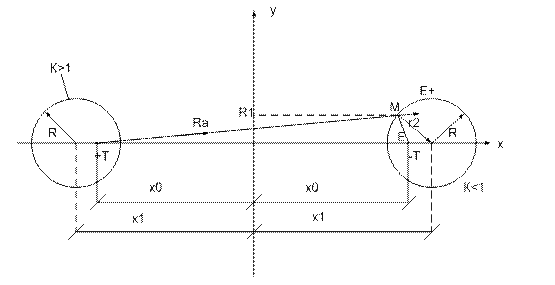 2x0 –
расстояние между осями.
2x0 –
расстояние между осями.
Результирующая
напряженность поля в точке М: 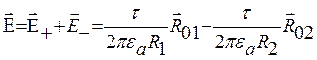
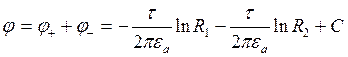
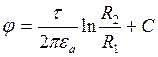 .
.
Если принять равенство нулю
кат-ка на оси у (при ![]() ), то
), то
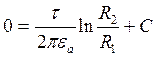 => C=0
=> C=0
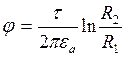
Определим потенциал точки М через ее координаты.
![]() ;
; ![]()
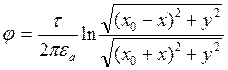
На рисунке окружности –
эквипотенциальные линии. Уравнения эквипотенциали ![]() =>
Для каждой эквипотенциали данной задачи выполняется:
=>
Для каждой эквипотенциали данной задачи выполняется: 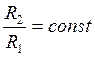 .
.
Обозначим 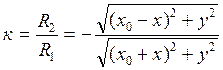 (*)
(*)
После некоторых преобразований выражения (*) получим величину радиуса эквипотенциальных окружностей.
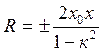
И координаты центра этих
окружностей:![]()
 .
.
В двух последних формулах ,знак (+) берется при к<1, т.е. для окружностей рассматриваемых в кривой полуплоскости, для к>1 в левой полуплоскости.
Найдем потенциал и емкость на ед. длинны двухпроводной линии передачи
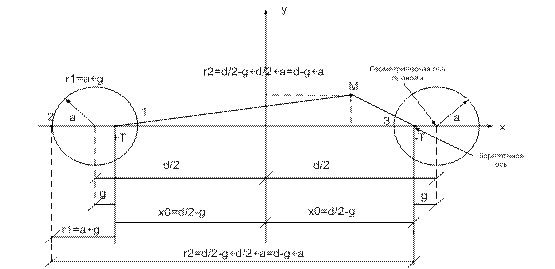
Поверхность проводника – эквипотенциальная. Внутри проводника поле отсутствует. Два исходных повода можно заменить двумя фиктивными заряженными зарядами и подобрать такое их расположение при котором эквипот. пов-ти фиктивных осей совпали бы с пов-ю проводов линии передачи. Тогда, согласно следствию (1) из т. Единственности, поля вне проводов будет таким же, как и поле фиктивных заряженных осей.
Дано: / Найти: g
а; d; ![]() /
/
Решение:
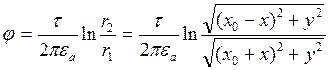 ;
;
![]() .
.
Для эквипот. поверхностей
выполняется 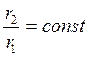 .
.
Рассматривая точки 1 и 2 получим:
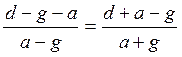 (*)
(*)
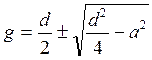
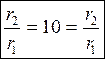 -
условия эквипотенциальности.
-
условия эквипотенциальности.
Потенциал в любай точке М:
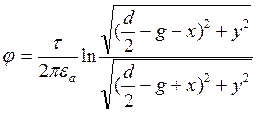 ;
;
Определим емкость на единицу
длинны линии: 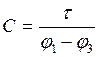 ;
;
Определим координаты точек 1 и 3
1) x=d/2-a; y=0
3) x=(-d/2-a); y=0
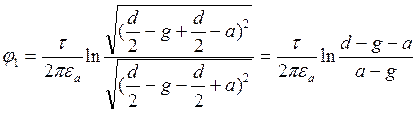 ;
;
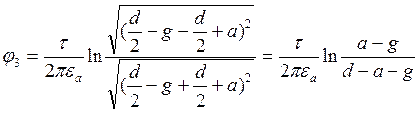 /
/
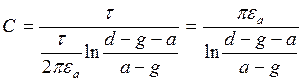 =>
=> 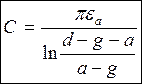
Если а>>g
d>>a 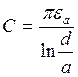 .
.
При расчете более сложных полей, используется непосредственное интегрирование ур-я Пуассона.
Общий порядок расчета состоит в следующем: в зависимости от вида задачи выбирают корд. систему если учесть удачным ее выбором удается представить потенциал в виде функции одной переменной, то ур-е в частных производных Пуассона (Лапласа), превращается в обыкновенное Д.У.
Если потенциал оказывается функцией 2-х или 3-х коорд., то обычно для решения ур-я в частных произв-х используют метод разделения переменных (м-д Фурье).
Затем по исходным данным и условиям на границе раздела сред определяют:
а) в случае обыкновенного Д.У. пост. интегр-я.
б) в случае ур-я в Ч.П. – функции удовл-е граничн. Условии.
Пример: Интегрирование ур-е Пуассона.
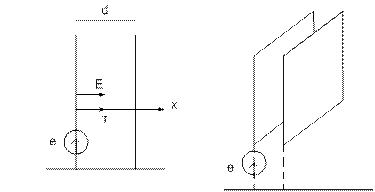
В вакууме находится 2 плоских электрода, причем их размеры много больше расстояния между электродами d/
Потенциал левого
электрода: ![]()
Потенциал правого
электрода: ![]()
В пространстве между электродами распределен объемный заряд, закон изменения объемной плотности кот.:
![]() , где
а = const
, где
а = const
Определить з-н изменения потенциала в пространстве между электродами.
Выбираем прямоугольную С.К., для кот. ур-е Пуассона имеет вид:
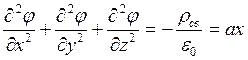
Поскольку в данной задачи, потенциал зависит только от одной координаты х, то ур-е обретает вид.
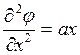 или
или 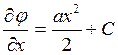
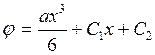 .
.
Определим постоянные интегрирования с помощью граничных условий.
При х = 0 ![]()
При х = d 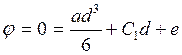
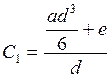
Тогда окончательно закон изменения потенциала имеет вид:
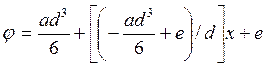 .
.
Определить закон изменения напряженности.
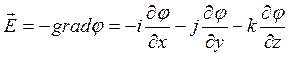
Учитывая зависимость потенциала только от коорд-ты х, получим
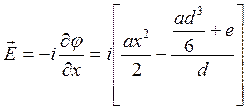
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.